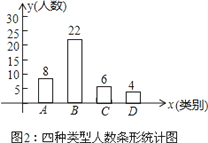
【题目】萧山北干初中组织外国教师(外教)进班上英语课,王明同学为了解全校学生对外教的喜爱程度,在全校随机抽取了若干名学生进行问卷调查.问卷将喜爱程度分为A(非常喜欢)、B(喜欢)、C(不太喜欢)、D(很不喜欢)四种类型,根据调查结果绘制成了两幅不完整的统计图,请结合统计图信息解答下列问题:

(1)这次调查中,一共调查了 名学生,图1中C类所对应的圆心角度数为 ;
(2)请补全条形统计图;
(3)在非常喜欢外教的5位同学(三男两女)中任意抽取两位同学作为交换生,请用列表法或画树状图求出恰好抽到一名男生和一名女生作为交换生的概率.
参考答案:
【答案】(1)40;54°;
(2)补全条形统计图见解析;
(3)树状图或列表见解析,P(一男一女)=![]()
【解析】试题分析:(1)通过D类型有4人占比10%即可得到调查的人数;然后根据条形图得到C类的人数,通过占比求得相应圆心角的度数;
(2)用调查的总人数减去A、B、D类的人数得到C类的人数,补全图形即可;
(3)通过列表法即可求得概率.
试题解析:(1)一共调查了4÷10%=40人,40-8-22-4=6,360°×![]() =54°,故填:40;54°;
=54°,故填:40;54°;
(2)补全条形统计图,如图所示:
(3)列表:
男1 | 男2 | 男3 | 女1 | 女2 | |
男1 | √ | √ | |||
男2 | √ | √ | |||
男3 | √ | √ | |||
女1 | √ | √ | √ | ||
女2 | √ | √ | √ |
所有等可能的情况有20种情况,其中一男一女的情况有12种,
则P(一男一女)=![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】若点A(a+2,b-1)在第二象限,则点B(-a,b-1)在( )
A. 第一象限 B. 第二象限 C. 第三象限 D. 第四象限
-
科目: 来源: 题型:
查看答案和解析>>【题目】平面直角坐标系内的点A(-1,2)与点B(-1,-2)的位置关系是( )
A. 关于y轴对称 B. 关于x轴对称 C. 关于原点对称 D. 无法确定
-
科目: 来源: 题型:
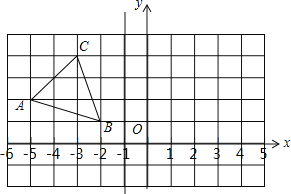
查看答案和解析>>【题目】在边长为1的小正方形组成的正方形网格中建立如图片所示的平面直角坐标系,已知格点三角形ABC(三角形的三个顶点都在小正方形上)
(1)画出△ABC关于直线l:x=﹣1的对称三角形△A1B1C1;并写出A1、B1、C1的坐标.
(2)在直线x=﹣l上找一点D,使BD+CD最小,满足条件的D点为 .
提示:直线x=﹣l是过点(﹣1,0)且垂直于x轴的直线.
-
科目: 来源: 题型:
查看答案和解析>>【题目】正方形四边条边都相等,四个角都是90°.如图,已知正方形ABCD在直线MN的上方,BC在直线MN上,点E是直线MN上一点,以AE为边在直线MN的上方作正方形AEFG.

(1)如图1,当点E在线段BC上(不与点B、C重合)时: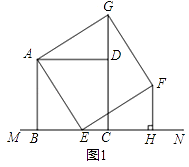
①判断△ADG与△ABE是否全等,并说明理由;
②过点F作FH⊥MN,垂足为点H,观察并猜测线段BE与线段CH的数量关系,并说明理由;
(2)如图2,当点E在射线CN上(不与点C重合)时: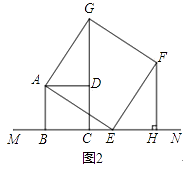
①判断△ADG与△ABE是否全等,不需说明理由;
②过点F作FH⊥MN,垂足为点H,已知GD=4,求△CFH的面积. -
科目: 来源: 题型:
查看答案和解析>>【题目】现有好友4人聚会,每两人握手一次,共握手次.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知反比例函数
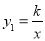 的图象与一次函数
的图象与一次函数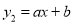 的图象交于点A(1,4)和点B(m,
的图象交于点A(1,4)和点B(m,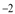 ).
).(1)求这两个函数的表达式;
(2)观察图象,当
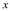 >0时,直接写出
>0时,直接写出 时自变量x的取值范围.
时自变量x的取值范围.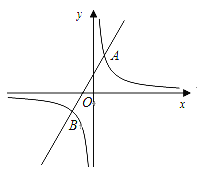
相关试题

