【题目】计算。
(1)填空:
(a﹣b)(a+b)=;
(a﹣b)(a2+ab+b2)=;
(a﹣b)(a3+a2b+ab2+b3)=;
(2)猜想:
(a﹣b)(an﹣1+an﹣2b+an﹣3b2+…+abn﹣2+bn﹣1)=(其中n为正整数,且n≥2);
(3)利用(2)猜想的结论计算:①29+28+27+…+22+2+1
②210﹣29+28﹣…﹣23+22﹣2.
参考答案:
【答案】
(1)a2﹣b2;a3﹣b3;a4﹣b4
(2)an﹣bn
(3)
解:①29+28+27+…+23+22+2+1=(2﹣1)(29+281+2712+…+2316+2217+218)+1
=210﹣110+1
=210﹣1+1
=1024;
②210﹣29+28﹣…+23﹣22+2
= ![]() ×[2﹣(﹣1)][210×(﹣1)0+29×(﹣1)1+27×(﹣1)2+…+23×(﹣1)7+22×(﹣1)8+2×(﹣1)9+20×(﹣1)10﹣1]
×[2﹣(﹣1)][210×(﹣1)0+29×(﹣1)1+27×(﹣1)2+…+23×(﹣1)7+22×(﹣1)8+2×(﹣1)9+20×(﹣1)10﹣1]
= ![]() [211﹣(﹣1)11﹣1]
[211﹣(﹣1)11﹣1]
= ![]() ×2048
×2048
= ![]()
【解析】解:(1)(a﹣b)(a+b)=a2﹣b2;
(a﹣b)(a2+ab+b2)=a3+a2b+ab2﹣a2b﹣ab2﹣b3=a3﹣b3;
(a﹣b)(a3+a2b+ab2+b3)=a4+a3b+a2b2+ab3﹣a3b﹣a2b2﹣ab3﹣b4=a4﹣b4;
所以答案是:a2﹣b2 , a3﹣b3 , a4﹣b4;(2)由(1)的规律可得:原式=an﹣bn ,
所以答案是:an﹣bn;
【考点精析】解答此题的关键在于理解数与式的规律的相关知识,掌握先从图形上寻找规律,然后验证规律,应用规律,即数形结合寻找规律.
-
科目: 来源: 题型:
查看答案和解析>>【题目】若y=(m+2)x|m|﹣1是正比例函数.(1)求m的值m=_____;(2)关系式是_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某公司有A、B两种客车,它们的载客量和租金如下表,星星中学根据实际情况,计划用A、B型车共5辆,同时送七年级师生到校基地参加社会实践活动.
A
B
载客量(人/辆)
40
20
租金(元/辆)
200
150
(1)若要保证租金费用不超过980元,请问该学校有哪几种租车方案?
(2)在(1)的条件下,若七年级师生共有150人,问哪种租车方案最省钱? -
科目: 来源: 题型:
查看答案和解析>>【题目】可以在箱子里先后摸出两个球(第一次摸出后不放回).商场根据两小球所标金额的和返还相等价格的购物券,购物券可以在本商场消费.某顾客刚好消费300元.
(1)该顾客至多可得到 元购物券;
(2)请你用画树状图或列表的方法,求出该顾客所获得购物券的金额不低于50元的概率.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1是一个三棱柱包装盒,它的底面是边长为10cm的正三角形,三个侧面都是矩形.现将宽为15cm的彩色矩形纸带AMCN裁剪成一个平行四边形ABCD(如图2),然后用这条平行四边形纸带按如图3的方式把这个三棱柱包装盒的侧面进行包贴(要求包贴时没有重叠部分),纸带在侧面缠绕三圈,正好将这个三棱柱包装盒的侧面全部包贴满.在图3中,将三棱柱沿过点A的侧棱剪开,得到如图4的侧面展开图.为了得到裁剪的角度,我们可以根据展开图拼接出符合条件的平行四边形进行研究.
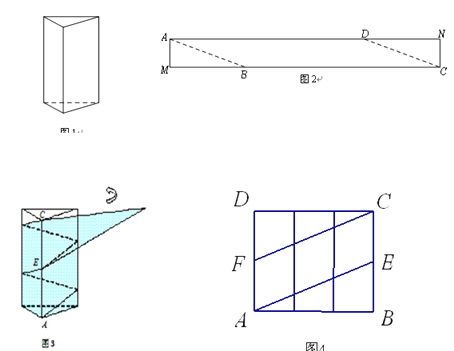
(1)请在图4中画出拼接后符合条件的平行四边形;
(2)请在图2中,计算裁剪的角度(即∠ABM的度数).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知等腰△ABC的周长是16,底边BC上的高AD的长是4,求这个三角形各边的长.
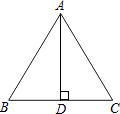
-
科目: 来源: 题型:
查看答案和解析>>【题目】关于x的方程(k+4)x2-2=0是关于x的一元二次方程,则k的取值范围是( )
A.k≠0
B.k≥4
C.k=-4
D.k≠-4
相关试题

