【题目】某生物兴趣小组在四天的实验研究中发现:骆驼的体温会随外部环境温度的变化而变化,而且在这四天中每昼夜的体温变化情况相同,他们将一头骆驼前两昼夜的体温变化情况绘制成右图,请根据图象回答:
(1)在这个问题中,自变量是什么?因变量是什么?
(2)第一天中,在什么时间范围内这头骆驼的体温是上升的?它的体温从最低上升到最高需要多少时间?
(3)第三天12时这头骆驼的体温是多少?

参考答案:
【答案】(1)自变量是外部环境温度;因变量是骆驼的体温;
(2)第一天中,从4时到16时这头骆驼的体温是上升的,它的体温从最低上升到最高需要12小时;
(3)第三天12时这头骆驼的体温是39℃.
【解析】
(1)根据题意即可得到结论;
(2)根据函数图象找出0~24小时图象随时间增大而增大的部分即可,然后求出从体温开始上升到上升结束的时间差即可;
(3)根据函数图象找出12时对应的体温值即可.
(1)在这个问题中,自变量是外部环境温度;因变量是骆驼的体温;
(2)由图可知,第一天中,从4时到16时这头骆驼的体温是上升的,
它的体温从最低上升到最高需要16-4=12小时;
(3)第三天12时这头骆驼的体温是39℃.
-
科目: 来源: 题型:
查看答案和解析>>【题目】把四张大小相同的长方形卡片(如图①)按图②、图③两种放法放在一个底面为长方形(长比宽多6)的盒底上,底面未被卡片覆盖的部分用阴影表示,若记图②中阴影部分的周长为C2,图③中阴影部分的周长为C3,则C2-C3=______.

-
科目: 来源: 题型:
查看答案和解析>>【题目】分解因式x2-4y2-2x+4y,细心观察这个式子就会发现,前两项符合平方差公式,后两项可提取公因式,前后两部分分别分解因式后会产生公因式,然后提取公因式就可以完成整个式子的分解因式,过程为:x2-4y2-2x+4y=(x+2y)(x-2y)-2(x-2y)=(x-2y)(x+2y-2).这种分解因式的方法叫分组分解法,利用这种方法解决下列问题:
(1)分解因式:a2-4a-b2+4;
(2)若△ABC三边a、b、c满足a2-ab-ac+bc=0,试判断△ABC的形状.
-
科目: 来源: 题型:
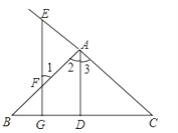
查看答案和解析>>【题目】看图填空:已知如图,AD⊥BC于D,EG⊥BC于G,∠E=∠1,
求证:AD平分∠BAC.
证明:∵AD⊥BC于D,EG⊥BC于G( 已知 )
∴∠ADC=90°,∠EGC=90°(___________)
∴∠ADC=∠EGC(等量代换)
∴AD∥EG(_____________)
∴∠1=∠2(___________)
∠E=∠3(___________)
又∵∠E=∠1( 已知)
∴∠2=∠3(___________)
∴AD平分∠BAC(___________).
-
科目: 来源: 题型:
查看答案和解析>>【题目】把一个图形先沿着一条直线进行轴对称变换,再沿着与这条直线平行的方向平移,我们把这样的图形变换叫做滑动对称变换.结合轴对称变换和平移变换的有关性质,你认为在滑动对称变换过程中,这两个对应三角形(如图)的对应点所具有的性质是( ).

A. 对应点所连线段都相等 B. 对应点所连线段被对称轴平分
C. 对应点连线与对称轴垂直 D. 对应点连线互相平行
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算题
(1)计算: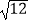 +|3﹣
+|3﹣  |﹣2sin60°+(2017﹣π)0+(
|﹣2sin60°+(2017﹣π)0+(  )﹣2
)﹣2
(2)解方程: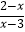 +
+ 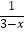 =1.
=1. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,边长为4的大正方形ABCD内有一个边长为1的小正方形CEFG,动点P以每秒1cm的速度从点A出发,沿A→D→E→F→G→B的路线绕多边形的边匀速运动到点B停止(不含点A和点B).设△ABP的面积为S,点P的运动时间为t.
(1)小颖通过认真的观察分析,得出了一个正确的结论:当点P在线段DE上运动时,存在着“同底等高”的现象,因此当点P在线段DE上运动时△ABP的面积S始终不发生变化.
问:在点P的运动过程中,还存在类似的现象吗?若存在,请说出P的位置;若不存在,请说明理由.
(2)在点P的运动过程中△ABP的面积S是否存在最大值?若存在,请求出最大面积;若不存在,请说明理由.
(3)请写出S与t之间的关系式.

相关试题

