【题目】如图所示,MN是⊙O的直径,作AB⊥MN,垂足为点D,连接AM,AN,点C为![]() 上一点,且
上一点,且![]() ,连接CM,交AB于点E,交AN于点F,现给出以下结论:①AD=BD;②∠MAN=90°;③
,连接CM,交AB于点E,交AN于点F,现给出以下结论:①AD=BD;②∠MAN=90°;③![]() ;④∠ACM+∠ANM=∠MOB;⑤AE=
;④∠ACM+∠ANM=∠MOB;⑤AE=![]() MF.
MF.
其中正确结论的个数是( )

A. 2 B. 3 C. 4 D. 5
参考答案:
【答案】D
【解析】根据垂径定理,由AB⊥MN可知AD=DB, ![]() ,故①③正确;根据直径所对的圆周角为直角,可由MN为直径,得到∠MAN=90°,故③正确;
,故①③正确;根据直径所对的圆周角为直角,可由MN为直径,得到∠MAN=90°,故③正确;
如图,
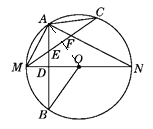
连接OA,由![]() ,得到∠MOB=∠MOA=2∠ACM=∠ACM+∠ANM,故④正确;
,得到∠MOB=∠MOA=2∠ACM=∠ACM+∠ANM,故④正确;
由![]() ,
, ![]() ,可得
,可得![]() ,所以可得∠AME=∠MAE,根据等角对等边,得到AE=ME,然后根据∠EAF+∠MAE=90°,等量代换得∠EFA+∠AME=90°,然后根据等角的余角相等,得到∠EAF=∠EFA,即AE=EF,然后可根据AE=EF=EM得到AE=
,所以可得∠AME=∠MAE,根据等角对等边,得到AE=ME,然后根据∠EAF+∠MAE=90°,等量代换得∠EFA+∠AME=90°,然后根据等角的余角相等,得到∠EAF=∠EFA,即AE=EF,然后可根据AE=EF=EM得到AE=![]() MF,故⑤正确.
MF,故⑤正确.
故选:D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,铁路MN和公路PQ在点O处交汇,∠QON=30°.公路PQ上A处距离O点240米.如果火车行驶时,周围200米以内会受到噪音的影响.那么火车在铁路MN上沿ON方向以72千米/时的速度行驶时,
(1)A处是否会受到火车的影响,并写出理由
(2)如果A处受噪音影响,求影响的时间.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正方形ABCD的对角线AC、BD相交于点O,正方形A′B′C′D′的顶点A′与点O重合,A′B′交BC于点E,A′D′交CD于点F.
(1)求证:OE=OF;
(2)若正方形ABCD的边长为1,求两个正方形重叠部分的面积;
(3)若正方形 A′B′C′D′绕着O点旋转,EF的长度何时最小,并求出最小值.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,
 是函数
是函数 上两点,
上两点, 为一动点,作
为一动点,作 轴,
轴, 轴,下列说法正确的是( )
轴,下列说法正确的是( )
①
 ;②
;② ;③若
;③若 ,则
,则 平分
平分 ;④若
;④若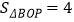 ,则
,则
A. ①③ B. ②③ C. ②④ D. ③④
-
科目: 来源: 题型:
查看答案和解析>>【题目】(2017怀化,第10题,4分)如图,A,B两点在反比例函数
 的图象上,C,D两点在反比例函数
的图象上,C,D两点在反比例函数 的图象上,AC⊥y轴于点E,BD⊥y轴于点F,AC=2,BD=1,EF=3,则
的图象上,AC⊥y轴于点E,BD⊥y轴于点F,AC=2,BD=1,EF=3,则 的值是( )
的值是( )
A. 6 B. 4 C. 3 D. 2
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图, 已知A(-4,-1),B(-5,-4),C(-1,-3),△ABC经过平移得到的△A′B′C′,△ABC中任意一点P(x1,y1)平移后的对应点为P′(x1+6,y1+4)。
(1)请在图中作出△A′B′C′;(2)写出点A′、B′、C′的坐标.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点P为定角∠AOB的平分线上的一个定点,且∠MPN与∠AOB互补,若∠MPN在绕点P旋转的过程中,其两边分别与OA、OB相交于M、N两点,则以下结论:(1)PM=PN恒成立;(2)OM+ON的值不变;(3)四边形PMON的面积不变;(4)MN的长不变,其中正确的个数为( )

A. 4B. 3C. 2D. 1
相关试题

