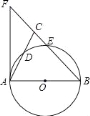
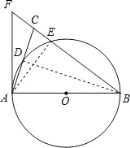
【题目】如图,在△ABC中,BA=BC,以AB为直径的⊙O分别交AC、BC于点D、E,BC的延长线于⊙O的切线AF交于点F.
(1)求证:∠ABC=2∠CAF;
(2)若AC=2![]() ,CE:EB=1:4,求CE的长.
,CE:EB=1:4,求CE的长.
参考答案:
【答案】(1)见解析;
(2)CE=2.
【解析】
试题分析:(1)首先连接BD,由AB为直径,可得∠ADB=90°,又由AF是⊙O的切线,易证得∠CAF=∠ABD.然后由BA=BC,证得:∠ABC=2∠CAF;
(2)首先连接AE,设CE=x,由勾股定理可得方程:(2![]() )2=x2+(3x)2求得答案.
)2=x2+(3x)2求得答案.
试题解析:(1)证明:如图,连接BD.∵AB为⊙O的直径,∴∠ADB=90°,∴∠DAB+∠ABD=90°.∵AF是⊙O的切线,∴∠FAB=90°,即∠DAB+∠CAF=90°.∴∠CAF=∠ABD.∵BA=BC,∠ADB=90°,
∴∠ABC=2∠ABD.∴∠ABC=2∠CAF.
(2)如图,连接AE,∴∠AEB=90°,设CE=x,∵CE:EB=1:4,
∴EB=4x,BA=BC=5x,AE=3x,在Rt△ACE中,AC2=CE2+AE2,
即(2![]() )2=x2+(3x)2,∴x=2.∴CE=2.
)2=x2+(3x)2,∴x=2.∴CE=2.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列语句错误的是( )
A. 延长线段AB
B. 延长射线AB
C. 直线m和直线n相交于点P
D. 在射线AB上截取线段AC,使AC=3 cm
-
科目: 来源: 题型:
查看答案和解析>>【题目】将方程化为一般形式:2x2-3x=3x-5是____________________
-
科目: 来源: 题型:
查看答案和解析>>【题目】某商店经销一种商品,由于进价降低了5%,出售价不变,使得利润由m%提高到(m+6)%,则m的值为( )
A.10
B.12
C.14
D.17 -
科目: 来源: 题型:
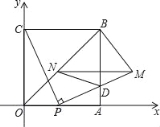
查看答案和解析>>【题目】如图,四边形OABC是边长为4的正方形,点P为OA边上任意一点(与点O、A不重合),连接CP,过点P作PM⊥CP交AB于点D,且PM=CP,过点M作MN∥OA,交BO于点N,连接ND、BM,设OP=t.
(1)求点M的坐标(用含t的代数式表示).
(2)试判断线段MN的长度是否随点P的位置的变化而改变?并说明理由.
(3)当t为何值时,四边形BNDM的面积最小.
-
科目: 来源: 题型:
查看答案和解析>>【题目】若关于x的方程3x+2m=1的解与方程-2x-1=5的解相同,则m的值为 ( )
A. 5 B. -5
C. 4 D. -4
-
科目: 来源: 题型:
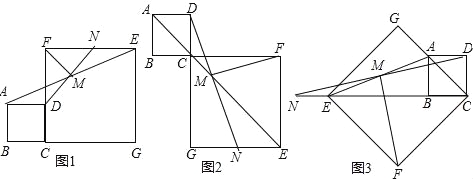
查看答案和解析>>【题目】如图1所示,在正方形ABCD和正方形CGEF中,点B、C、G在同一条直线上,M是线段AE的中点,DM的延长线交EF于点N,连接FM,易证:DM=FM,DM⊥FM(无需写证明过程)
(1)如图2,当点B、C、F在同一条直线上,DM的延长线交EG于点N,其余条件不变,试探究线段DM与FM有怎样的关系?请写出猜想,并给予证明;
(2)如图3,当点E、B、C在同一条直线上,DM的延长线交CE的延长线于点N,其余条件不变,探究线段DM与FM有怎样的关系?请直接写出猜想.
相关试题

