【题目】如图,B、D、E在一条直线上,AB=AC,AD=AE,∠BAC=∠DAE,
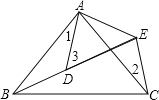
(1)求证:BD=CE
(2)猜想∠1、∠2、∠3的数量关系,并说明理由.
参考答案:
【答案】(1)见解析;(2)∠3=∠1+∠2,理由见解析.
【解析】
(1)首先求出∠BAD =∠CAE,然后利用SAS证明△BAD≌△CAE可得BD=CE;
(2)根据全等三角形对应角相等求出∠ABD=∠2,由三角形外角的性质可得∠3=∠1+∠2.
(1)∵∠BAC=∠DAE,
∴∠BAC-∠DAC=∠DAE-∠DAC,即∠BAD =∠CAE,
在△BAD和△CAE中, ,
,
∴△BAD≌△CAE(SAS),
∴BD=CE;
(2)∠3=∠1+∠2,
理由:∵△BAD≌△CAE,
∴∠ABD=∠2,
∵∠3=∠1+∠ABD,
∴∠3=∠1+∠2.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,
 ,作
,作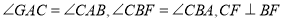 垂足为点
垂足为点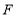 ,
,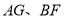 相交于点
相交于点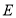 .
.
(1)求
 的度数.
的度数.(2)求证:

-
科目: 来源: 题型:
查看答案和解析>>【题目】用直尺和圆规画一个角等于已知角,是运用了“全等三角形的对应角相等”这一性质,其全等的依据是( )

A.SAS B.ASA C.AAS D.SSS
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,点F从菱形ABCD的顶点A出发,沿A→D→B以1cm/s的速度匀速运动到点B,图2是点F运动时,△FBC的面积y(cm2)随时间x(s)变化的关系图象,则a的值为( )

A.
 B. 2 C.
B. 2 C.  D. 2
D. 2
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,已知 AD 是△ABC 的边 BC 上的中线.
(1)作出△ABD 的边 BD 上的高.
(2)若△ABC 的面积为 10,求△ADC 的面积.
(3)若△ABD 的面积为 6,且 BD 边上的高为 3,求 BC 的长.

-
科目: 来源: 题型:
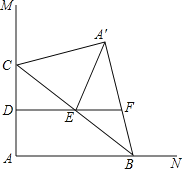
查看答案和解析>>【题目】如图,∠MAN=90°,点C在边AM上,AC=4,点B为边AN上一动点,连接BC,△A′BC与△ABC关于BC所在直线对称,点D,E分别为AC,BC的中点,连接DE并延长交A′B所在直线于点F,连接A′E.当△A′EF为直角三角形时,AB的长为_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,△ABC的边BC在直线l上,AC⊥BC,且AC=BC,△EFP的边FP也在直线l上,边EF与边AC重合,且EF=FP.
(1)直接写出AB与AP所满足的数量关系:_____,AB与AP的位置关系:_____;
(2)将△ABC沿直线l向右平移到图2的位置时,EP交AC于点Q,连接AP,BQ,求证:AP=BQ;
(3)将△ABC沿直线l向右平移到图3的位置时,EP的延长线交AC的延长线于点Q,连接AP,BQ,试探究AP=BQ是否仍成立?并说明理由.

相关试题

