【题目】如图,![]() 、
、![]() 分别为数轴上的两点,
分别为数轴上的两点,![]() 点对应的数为-5,
点对应的数为-5,![]() 点对应的数为55.现有一动点
点对应的数为55.现有一动点![]() 以6个单位/秒的速度从
以6个单位/秒的速度从![]() 点出发,同时另一动点
点出发,同时另一动点![]() 恰好以4个单位/秒的速度从
恰好以4个单位/秒的速度从![]() 点出发:
点出发:

(1)若![]() 向左运动,同时
向左运动,同时![]() 向右运动,在数轴上的
向右运动,在数轴上的![]() 点相遇,求
点相遇,求![]() 点对应的数.
点对应的数.
(2)若![]() 向左运动,同时
向左运动,同时![]() 向左运动,在数轴上的
向左运动,在数轴上的![]() 点相遇,求
点相遇,求![]() 点对应的数.
点对应的数.
(3)若![]() 向左运动,同时
向左运动,同时![]() 向右运动,当
向右运动,当![]() 与
与![]() 之间的距离为20个单位长度时,求此时
之间的距离为20个单位长度时,求此时![]() 点所对应的数.
点所对应的数.
参考答案:
【答案】(1)19;(2)-125;(3)11.
【解析】
(1)首先求出A、B两点之间的距离,然后求出相遇时间,再求出点Q所走的路程,根据左减右加的原则,可求出相遇地点所对应的数;
(2)此题是追及问题,先求出P追上Q所需的时间,然后求出Q所走的路程,根据左减右加的原则,可求出点D所对应的数;
(3)首先设其运动时间为t,根据题意列出关系式,解得t,然后求出Q点运动的路程,即可求出Q此时对应的数.
(1)∵![]() 点对应的数为-5,
点对应的数为-5,![]() 点对应的数为55
点对应的数为55
∴A、B两点之间的距离是55-(-5)=60
它们相遇的时间是60÷(6+4)=6
即相同时间Q点运动路程是4×6=24
即从数-5向右运动24个单位到19
即C点对应的数是19;
(2)P点追到Q点的时间是60÷(6-4)=30
即此时Q点运动的路程是4×30=120
即从数-5向左运动120个单位到数-125
即D点对应的数为-125.
(3)设其运动时间为t,则
4t+6t+20=60
解得t=4
即Q点运动的路程是4×4=16
即Q点从数-5向右运动16个单位到数11
即Q点此时对应的数是11.
-
科目: 来源: 题型:
查看答案和解析>>【题目】小虫从某点
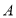 出发在一条直线上来回爬行,规定向右爬行的路程记为正数,向左爬行的路程记为负数,爬行的各段路程依次记为(单位:
出发在一条直线上来回爬行,规定向右爬行的路程记为正数,向左爬行的路程记为负数,爬行的各段路程依次记为(单位: )-11、+8、+9、-3、-6、+12、-9.
)-11、+8、+9、-3、-6、+12、-9.(1)小虫最后中否回到出发点,请判断并且通过计算说明理由.
(2)在爬行的过程中,如果每爬行一个单位长度奖励一粒芝麻,则整个运动过程中小虫一共得到多少粒芝麻?
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,在梯形ABCD中,AB∥CD,∠D=90°,AD=CD=2,点E在边AD上(不与点A、D重合),∠CEB=45°,EB与对角线AC相交于点F,设DE=x.
(1)用含x的代数式表示线段CF的长;
(2)如果把△CAE的周长记作C△CAE,△BAF的周长记作C△BAF,设
 =y,求y关于x的函数关系式,并写出它的定义域;
=y,求y关于x的函数关系式,并写出它的定义域;(3)当∠ABE的正切值是
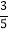 时,求AB的长.
时,求AB的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,四边形
 和
和 分别是边长为
分别是边长为 和
和 的正方形.
的正方形.
(1)用含
 和
和 的代数式表示图中三角形
的代数式表示图中三角形 的面积.
的面积.(2)用用
 和
和 的代数式表示图中阴影部分的面积.
的代数式表示图中阴影部分的面积.(3)小军计算出当
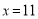 ,
, 时的阴影部分面积,与小明计算的当
时的阴影部分面积,与小明计算的当 ,
, 时的阴影部分面积相等,为什么呢?请说明理由,并求出此时的阴影部分面积.
时的阴影部分面积相等,为什么呢?请说明理由,并求出此时的阴影部分面积. -
科目: 来源: 题型:
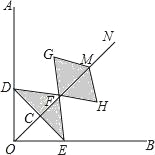
查看答案和解析>>【题目】如图,在Rt∠AOB的平分线ON上依次取点C,F,M,过点C作DE⊥OC,分别交OA,OB于点D,E,以FM为对角线作菱形FGMH.已知∠DFE=∠GFH=120°,FG=FE,设OC=x,图中阴影部分面积为y,则y与x之间的函数关系式是( )
A. y=
 B. y=
B. y=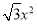 C. y=2
C. y=2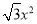 D. y=3
D. y=3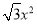
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图是二次函数y=ax2+bx+c图象的一部分,图象过点A(﹣3,0),对称轴为直线x=﹣1,给出以下结论:①abc<0 ②b2﹣4ac>0 ③4b+c<0 ④若B(﹣
 ,y1)、C(﹣
,y1)、C(﹣ ,y2)为函数图象上的两点,则y1>y2⑤当﹣3≤x≤1时,y≥0,
,y2)为函数图象上的两点,则y1>y2⑤当﹣3≤x≤1时,y≥0,其中正确的结论是(填写代表正确结论的序号)__________________.

-
科目: 来源: 题型:
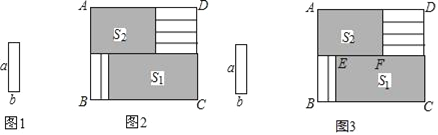
查看答案和解析>>【题目】将6张小长方形纸片(如图1所示)按图2所示的方式不重叠的放在长方形ABCD内,未被覆盖的部分恰好分割为两个长方形,面积分别为S1和S2.已知小长方形纸片的长为a,宽为b,且a>b.当AB长度不变而BC变长时,将6张小长方形纸片还按照同样的方式放在新的长方形ABCD内,S1与S2的差总保持不变,求a,b满足的关系式.
(1)为解决上述问题,如图3,小明设EF=x,则可以表示出S1=_________,S2=_________;
(2)求a,b满足的关系式,写出推导过程.
相关试题

