【题目】如图,点C在AB上,点M、N分别是AC、BC的中点,
(1)若AC=12cm,BC=10cm,求线段MN的长;
(2)若点C为线段AB上任意一点,满足AC+BC=acm,其它条件不变,你能猜想MN的长度吗?并说明理由;
(3)若点C在线段AB的延长线上,且满足AC-BC=bcm,点M、N分别为AC、BC的中点,你能猜想MN的长度吗?请画出图形,并说明理由.请用一句简洁的话描述你发现的结论.
![]()
参考答案:
【答案】(1)11(2)MN=![]() (3)MN=
(3)MN=![]()
【解析】
(1)根据线段中点的性质,可得MC、CN,再根据线段的和差,可得答案;
(2)根据线段中点的性质,可得MC、CN,再根据线段的和差,可得答案;
(3)根据线段中点的性质,可得MC、CN,再根据线段的和差,可得答案.
(1)由M、N分别是AC、BC的中点,
得MC=![]() AC,CN=
AC,CN=![]() BC.
BC.
由线段的和差,得MN=MC+CN=![]() AC+
AC+![]() BC=
BC=![]() ×12+
×12+![]() ×10=6+5=11cm;
×10=6+5=11cm;
(2)MN=![]() ,理由如下:
,理由如下:
由M、N分别是AC、BC的中点,
得MC=![]() AC,CN=
AC,CN=![]() BC.
BC.
由线段的和差,得MN=MC+CN=![]() AC+
AC+![]() BC=
BC=![]() (AC+BC)=
(AC+BC)=![]() cm;
cm;
(3)MN=![]() ,理由如下:
,理由如下:
由M、N分别是AC、BC的中点,
得MC=![]() AC,CN=
AC,CN=![]() BC.
BC.
由线段的和差,得MN=MC-CN=![]() AC-
AC-![]() BC=
BC=![]() (AC-BC)=
(AC-BC)=![]() cm;
cm;
如图:
![]() ,
,
只要满足点C在线段AB所在直线上,点M、N分别是AC、BC的中点.那么MN就等于AB的一半.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,Rt△AB′C′是由Rt△ABC绕点A顺时针旋转得到的,连接CC′交斜边于点E,CC′的延长线交BB′于点F.
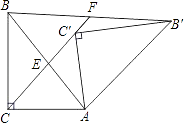
(1)证明:△ACE∽△FBE;
(2)设∠ABC=α,∠CAC′=β,试探索α、β满足什么关系时,△ACE与△FBE是全等三角形,并说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,把△ABC沿EF翻折,叠合后的图形如图.若∠A=60°,∠1=95°,则∠2的度数为________.

-
科目: 来源: 题型:
查看答案和解析>>【题目】在我们学习过的数学教科书中,有一个数学活动,其具体操作过程是:
第一步:对折矩形纸片ABCD,使AD与BC重合,把纸片展开,得到折痕EF(如图1);
第二步:再一次折叠纸片,使点A落在EF上,并使折痕经过点B,得到折痕BM,同时得到线段BN(如图2).
请解答以下问题:
(1)如图2,若延长MN交BC于P,△BMP是什么三角形?请证明你的结论;
(2)在图2中,若AB=a,BC=b,a、b满足什么关系,才能在矩形纸片ABCD上剪出符合(1)中结论的三角形纸片BMP?
(3)设矩形ABCD的边AB=2,BC=4,并建立如图3所示的直角坐标系.设直线BM′为y=kx,当∠M′BC=60°时,求k的值.此时,将△ABM′沿BM′折叠,点A是否落在EF上(E、F分别为AB、CD中点),为什么? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正五边形ABCDE放入某平面直角坐标系后,若顶点A,B,C,D的坐标分别是(0,a),(﹣3,2),(b,m),(c,m),则点E的坐标是( )

A.(2,﹣3)
B.(2,3)
C.(3,2)
D.(3,﹣2) -
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示的数表是由1开始的连续自然数排列而成的,根据你观察的规律完成下面问题:
(1)第8行最后一个数是________;第n行共有__________个数,这行第一个数是__________,这行最后一个数是______________.
(2)求第10行各数的和.

相关试题

