【题目】如图,将Rt△ABC绕直角顶点C顺时针旋转90°,得到△A′B′C,若∠B=60°,则∠1的度数是( )

A.15° B.25° C.10° D.20°
参考答案:
【答案】A
【解析】
试题分析:先利用互余计算出∠BAC=90°﹣∠B=30°,再根据旋转的性质得∠ACA′=90°,CA=CA′,∠CA′B′=∠CAB=30°,则可判断△ACA′为等腰直角三角形,则∠CA′A=45°,然后利用∠1=∠CA′A﹣∠CA′B′进行计算即可.
解:∵∠ACB=90°,∠B=60°,
∴∠BAC=90°﹣∠B=30°,
∵Rt△ABC绕直角顶点C顺时针旋转90°,得到△A′B′C,
∴∠ACA′=90°,CA=CA′,∠CA′B′=∠CAB=30°,
∴△ACA′为等腰直角三角形,
∴∠CA′A=45°,
∴∠1=∠CA′A﹣∠CA′B′=45°﹣30°=15°.
故选A.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中,AB=AC,AB的垂直平分线交边AB于D点,交边AC于E点,若△ABC与△EBC的周长分别是40cm,24cm,则AB= cm.

-
科目: 来源: 题型:
查看答案和解析>>【题目】计划在某广场内种植A、B两种花木共6600棵,若A花木数量是B花木数量的2倍少600棵.
(1)A、B两种花木的数量分别是多少棵?
(2)如果园林处安排26人同时种植这两种花木,每人每天能种植A花木610棵或B花木40棵,应分别安排多少人种植A花木和B花木,才能确保同时完成各自的任务?
-
科目: 来源: 题型:
查看答案和解析>>【题目】用代数式表示“2m与5的差”为( )
A. 2m-5 B. 5-2m C. 2(m-5) D. 2(5-m)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形ABCD是⊙O的内接四边形,BC的延长线与AD的延长线交于点E,且DC=DE.
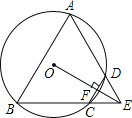
(1)求证:∠A=∠AEB;
(2)连接OE,交CD于点F,OE⊥CD,求证:△ABE是等边三角形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(2016浙江省温州市第7题)六边形的内角和是( )
A.540° B.720° C.900° D.1080°
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列各组中的两个单项式中,是同类项的是( )
A.a2和-2a B.2m2n和3nm2
C.-5ab和-5abc D.x3和23
相关试题

