【题目】如图,正方形ABCO的边OA、OC在坐标轴上,点B坐标为(8,8),将正方形ABCO绕点C逆时针旋转角度α(0°<α<90°),得到正方形CDEF,ED交线段AB于点G,ED的延长线交线段OA于点H,连CH、CG.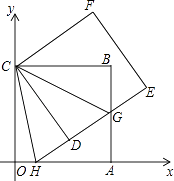
(1)求证:△CBG≌△CDG;
(2)求∠HCG的度数;判断线段HG、OH、BG的数量关系,并说明理由;
(3)连结BD、DA、AE、EB得到四边形AEBD,在旋转过程中,四边形AEBD能否为矩形?如果能,请求出点H的坐标;如果不能,请说明理由.
参考答案:
【答案】
(1)∵正方形ABCO绕点C旋转得到正方形CDEF,
∴CD=CB,∠CDG=∠CBG=90°.
在Rt△CDG和Rt△CBG中,
![]() ,
,
∴△CDG≌△CBG(HL)
(2)解:∵△CDG≌△CBG,
∴∠DCG=∠BCG,DG=BG.
在Rt△CHO和Rt△CHD中,
∵ ![]() ,
,
∴△CHO≌△CHD(HL),
∴∠OCH=∠DCH,OH=DH,
∴∠HCG=∠HCD+∠GCD= ![]() ∠OCD+
∠OCD+ ![]() ∠DCB=
∠DCB= ![]() ∠OCB=45°,
∠OCB=45°,
∴HG=HD+DG=HO+BG
(3)解:四边形AEBD可为矩形.
如图,连接BD、DA、AE、EB, 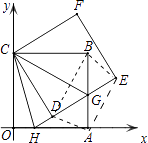
四边形AEBD若为矩形,则需先为平行四边形,即要对角线互相平分,合适的点只有G为AB中点的时候.
∵DG=BG,
∴DG=AG=EG=BG,即平行四边形AEBD对角线相等,则其为矩形,
∴当G点为AB中点时,四边形AEBD为矩形.
∵四边形DAEB为矩形,
∴AG=EG=BG=DG.
∵AB=6,
∴AG=BG=3.
设H点的坐标为(x,0),则HO=x
∵OH=DH,BG=DG,
∴HD=x,DG=3.
在Rt△HGA中,
∵HG=x+3,GA=3,HA=6﹣x,
∴(x+3)2=32+(6﹣x)2,解得x=2.
∴H点的坐标为(2,0).
【解析】(1)根据旋转的性质正方形ABCO绕点C旋转得到正方形CDEF,,得到对应边、对应角相等,得到△CDG≌△CBG;(2)由(1)知△CDG≌△CBG,得到对应边、对应角相等,得到△CHO≌△CHD,根据全等三角形的对应边、对应角相等,得到∠OCH=∠DCH,OH=DH,由正方形的性质,得到HG=HD+DG=HO+BG;(3)根据四边形AEBD若为矩形,则需先为平行四边形,即要对角线互相平分,合适的点只有G为AB中点的时候,由DG=BG,得到DG=AG=EG=BG,即平行四边形AEBD对角线相等,则其为矩形,当G点为AB中点时,四边形AEBD为矩形;再根据勾股定理求出H点的坐标.
【考点精析】根据题目的已知条件,利用正方形的性质的相关知识可以得到问题的答案,需要掌握正方形四个角都是直角,四条边都相等;正方形的两条对角线相等,并且互相垂直平分,每条对角线平分一组对角;正方形的一条对角线把正方形分成两个全等的等腰直角三角形;正方形的对角线与边的夹角是45o;正方形的两条对角线把这个正方形分成四个全等的等腰直角三角形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】若x2+kx+25是一个完全平方式,则k的值是____________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】网上购物已经成为人们常用的一种购物方式,售后评价特别引人关注,消费者在网店购买某种商品后,对其有“好评”、“中评”、“差评”三种评价,假设这三种评价是等可能的.
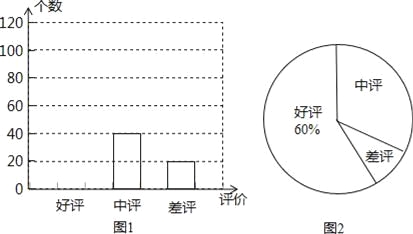
(1)小明对一家网店销售某种商品显示的评价信息进行了统计,并列出了两幅不完整的统计图.
利用图中所提供的信息解决以下问题:
①小明一共统计了 个评价;
②请将图1补充完整;
③图2中“差评”所占的百分比是 ;
(2)若甲、乙两名消费者在该网店购买了同一商品,请你用列表格或画树状图的方法帮助店主求一下两人中至少有一个给“好评”的概率.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在绘制频数直方图时,若有50个数据,其中最大值为38,最小值为16,取组距为4,则应该分( )
A.4组
B.5组
C.6组
D.7组 -
科目: 来源: 题型:
查看答案和解析>>【题目】(8分)一次函数
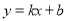 与反比例函数
与反比例函数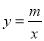 的图象相交于A(﹣1,4),B(2,n)两点,直线AB交x轴于点D.
的图象相交于A(﹣1,4),B(2,n)两点,直线AB交x轴于点D.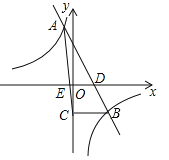
(1)求一次函数与反比例函数的表达式;
(2)过点B作BC⊥y轴,垂足为C,连接AC交x轴于点E,求△AED的面积S.
-
科目: 来源: 题型:
查看答案和解析>>【题目】列频数分布表考查50名学生年龄时,这些学生的年龄落在5个小组中,第一、二、三、五组的数据个数分别是1,9,15,5,则第四组的频数是( )
A.10
B.9
C.15
D.20 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系xOy中,点A(1,3),点B(5,1).
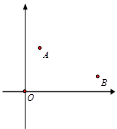
(1)只用直尺(无刻度)和圆规,求作一个点P,使点P同时满足下列两个条件:①点P到A,B两点的距离相等; ②点P到∠xOy的两边的距离相等.(要求保留作图痕迹,不必写出作法)
(2)在(1)作出点P后,点P的坐标为 .
相关试题

