【题目】如图,反比例函数![]() 与一次函数y=ax+b的图象交于点A(2,2)、B(
与一次函数y=ax+b的图象交于点A(2,2)、B(![]() ,n).
,n).
(1)求这两个函数解析式;
(2)将一次函数y=ax+b的图象沿y轴向下平移m个单位,使平移后的图象与反比例函数![]() 的图象有且只有一个交点,求m的值.
的图象有且只有一个交点,求m的值.

参考答案:
【答案】(1)![]() ,y=﹣4x+10;(2)m=2或m=18.
,y=﹣4x+10;(2)m=2或m=18.
【解析】
试题分析:(1)由点A在反比例函数的图象上,结合反比例函数图象上的点的坐标特征即可得出反比例函数的解析式;由点B的横坐标以及反比例函数的解析式即可得出点B的坐标,再由A、B点的坐标利用待定系数法即可求出一次函数得解析式;
(2)结合(1)中得结论找出平移后的直线的解析式,将其代入反比例函数解析式中,整理得出关于x的二次方程,令其根的判别式△=0,即可得出关于m的一元二次方程,解方程即可得出结论.
试题解析:(1)∵A(2,2)在反比例函数![]() 的图象上,∴k=4,∴反比例函数的解析式为
的图象上,∴k=4,∴反比例函数的解析式为![]() .
.
又∵点B(![]() ,n)在反比例函数
,n)在反比例函数![]() 的图象上,∴
的图象上,∴![]() ,解得:n=8,即点B的坐标为(
,解得:n=8,即点B的坐标为(![]() ,8).
,8).
由A(2,2)、B(![]() ,8)在一次函数y=ax+b的图象上,得:
,8)在一次函数y=ax+b的图象上,得: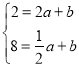 ,解得:
,解得:![]() ,∴一次函数的解析式为y=﹣4x+10.
,∴一次函数的解析式为y=﹣4x+10.
(2)将直线y=﹣4x+10向下平移m个单位得直线的解析式为y=﹣4x+10﹣m,∵直线y=﹣4x+10﹣m与双曲线![]() 有且只有一个交点,令
有且只有一个交点,令![]() ,得
,得![]() ,∴△=
,∴△=![]() ,解得:m=2或m=18.
,解得:m=2或m=18.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在⊙O中,AB为直径,D.E为圆上两点,C为圆外一点,且∠E+∠C=90°.
(1)求证:BC为⊙O的切线.
(2)若sinA=
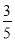 ,BC=6,求⊙O的半径.
,BC=6,求⊙O的半径.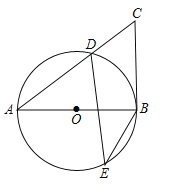
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,把函数y=x的图象上各点的纵坐标变为原来的2倍,横坐标不变,得到函数y=2x的图象;也可以把函数y=x的图象上各点的横坐标变为原来的
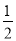 倍,纵坐标不变,得到函数y=2x的图象.
倍,纵坐标不变,得到函数y=2x的图象.类似地,我们可以认识其他函数.
(1)把函数
 的图象上各点的纵坐标变为原来的 倍,横坐标不变,得到函数
的图象上各点的纵坐标变为原来的 倍,横坐标不变,得到函数 的图象;也可以把函数
的图象;也可以把函数 的图象上各点的横坐标变为原来的 倍,纵坐标不变,得到函数
的图象上各点的横坐标变为原来的 倍,纵坐标不变,得到函数 的图象.
的图象.(2)已知下列变化:①向下平移2个单位长度;②向右平移1个单位长度;③向右平移
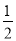 个单位长度;④纵坐标变为原来的4倍,横坐标不变;⑤横坐标变为原来的
个单位长度;④纵坐标变为原来的4倍,横坐标不变;⑤横坐标变为原来的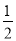 倍,纵坐标不变;⑥横坐标变为原来的2倍,纵坐标不变.
倍,纵坐标不变;⑥横坐标变为原来的2倍,纵坐标不变.(Ⅰ)函数
 的图象上所有的点经过④→②→①,得到函数 的图象;
的图象上所有的点经过④→②→①,得到函数 的图象;(Ⅱ)为了得到函数
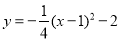 的图象,可以把函数
的图象,可以把函数 的图象上所有的点 .
的图象上所有的点 .A.①→⑤→③B.①→⑥→③C.①→②→⑥D.①→③→⑥
(3)函数
 的图象可以经过怎样的变化得到函数
的图象可以经过怎样的变化得到函数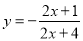 的图象?(写出一种即可)
的图象?(写出一种即可)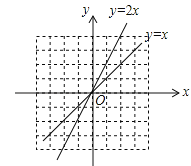
-
科目: 来源: 题型:
查看答案和解析>>【题目】若点P是第二象限内的点,且点P到x轴的距离是4,到y轴的距离是3,则点P的坐标是( )
A.(﹣4,3)
B.(4,﹣3)
C.(﹣3,4)
D.(3,﹣4) -
科目: 来源: 题型:
查看答案和解析>>【题目】某药品研究所开发一种抗菌新药,经多年动物实验,首次用于临床人体试验,测得成人服药后血液中药物浓度y(微克/毫升)与服药时间x小时之间函数关系如图所示(当4≤x≤10时,y与x成反比例).
(1)根据图象分别求出血液中药物浓度上升和下降阶段y与x之间的函数关系式.
(2)问血液中药物浓度不低于4微克/毫升的持续时间多少小时?

-
科目: 来源: 题型:
查看答案和解析>>【题目】下列调查中最适合普遍调查的是( )
A.调查某品牌灯泡的使用寿命B.调查振兴区居民网上购物情况
C.调查锦江山上各种鸟的总数量D.调查我国大型客机C919的零件质量
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图1,△ACB和△DCE均为等边三角形,点A、D、E在同一直线上,连接BE.

(1)求证:AD=BE;
(2)求∠AEB的度数;
(3)拓展探究:如图2,△ACB和△DCE均为等腰直角三角形,∠ACB=∠DCE=90°,点A、D、E在同一直线上,CM为△DCE中DE边上的高,连接BE. ①∠AEB的度数为°;
②探索线段CM、AE、BE之间的数量关系为 . (直接写出答案,不需要说明理由)
相关试题

