Question

【题目】如图，已知点E在直角△ABC的斜边AB上，以AE为直径的⊙O与直角边BC相切于点D．

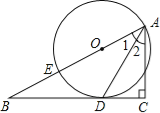
（1）求证：AD平分∠BAC；

（2）若BE=2，BD=4，求⊙O的半径．

Answer 1

【答案】（1）通过证明，得AD平分∠BAC （2）半径是3

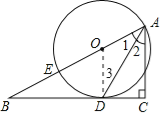
【解析】试题分析：（1）先连接OD，再由OD⊥BC和AC⊥BC可知OD∥AC从而得证；

（2）利用切割线定理可先求出AB，进而求出圆的直径，半径则可求出．

（1）证明：连接OD，

∵BC是⊙O的切线，

∴OD⊥BC，

又∵AC⊥BC，

∴OD∥AC，

∴∠2=∠3；

∵OA=OD，

∴∠1=∠3，

∴∠1=∠2，

∴AD平分∠BAC；

（2）解：∵BC与圆相切于点D．

∴BD2=BEBA，

∵BE=2，BD=4，

∴BA=8，

∴AE=AB﹣BE=6，

∴⊙O的半径为3．