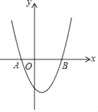
【题目】如图,在平面直角坐标系中抛物线y=(x+1)(x﹣3)与x轴相交于A、B两点,若在抛物线上有且只有三个不同的点C1、C2、C3,使得△ABC1、△ABC2、△ABC3的面积都等于m,则m的值是( )
A. 6 B. 8 C. 12 D. 16
参考答案:
【答案】B
【解析】
根据题目中的函数解析式可以求得该抛物线与x轴的交点坐标和顶点的坐标,再根据在抛物线上有且只有三个不同的点C1、C2、C3,使得△ABC1、△ABC2、△ABC3的面积都等于m,可知其中一点一定在顶点处,从而可以求得m的值.
∵抛物线y=(x+1)(x-3)与x轴相交于A、B两点,
∴点A(-1,0),点B(3,0),该抛物线的对称轴是直线x=![]() =1,
=1,
∴AB=3-(-1)=4,该抛物线顶点的纵坐标是:y=(1+1)×(1-3)=-4,
∵在抛物线上有且只有三个不同的点C1、C2、C3,使得△ABC1、△ABC2、△ABC3的面积都等于m,
∴m=![]() =8,
=8,
故选B.
-
科目: 来源: 题型:
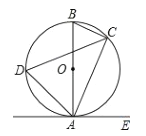
查看答案和解析>>【题目】如图,已知AB是⊙O的直径,点C、D在⊙O的上,点E在⊙O的外,∠EAC=∠D=60°.
(1)求∠ABC的度数;
(2)求证:AE是⊙O的切线.
-
科目: 来源: 题型:
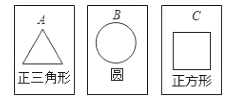
查看答案和解析>>【题目】如图,有三张背面完全相同的纸牌A、B、C,其中正面分别画有三种不同的几何图形,小华将这3张纸牌背面朝上洗匀后摸出一张,放回洗匀后再摸出一张,请你用画树状图或列表的方法,求摸出的两张纸牌面上所画几何图形既是轴对称图形又是中心对称图形的概率.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某商场销售一种品牌羽绒服和防寒服,其中羽绒服的售价是防寒服售价的5倍还多100元,2014年1月份(春节前期)共销售500件,羽绒服与防寒服销量之比是4:1,销售总收入为58.6万元.
(1)求羽绒服和防寒服的售价;
(2)春节后销售进入淡季,2014年2月份羽绒服销量下滑了6m%,售价下滑了4m%,防寒服销量和售价都维持不变,结果销售总收入下降为16.04万元,求m的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图是二次函数y=ax2+bx+c图象的一部分,图象过点A(﹣3,0),对称轴为直线x=﹣1,给出四个结论:①c>0;②若B(﹣
 ,y1),C(﹣
,y1),C(﹣ ,y2)为图象上的两点,则y1<y2;③2a﹣b=0;④
,y2)为图象上的两点,则y1<y2;③2a﹣b=0;④ <0,其中正确的结论是_____.
<0,其中正确的结论是_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知抛物线y=﹣x2+bx+c与一直线相交于A(1,0)、C(﹣2,3)两点,与y轴交于点N,其顶点为D.
(1)求抛物线及直线AC的函数关系式;
(2)若P是抛物线上位于直线AC上方的一个动点,求△APC的面积的最大值及此时点P的坐标;
(3)在对称轴上是否存在一点M,使△ANM的周长最小.若存在,请求出M点的坐标和△ANM周长的最小值;若不存在,请说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知二次函数y=ax2+bx+c,当x=3时,y有最小值﹣4,且图象经过点(﹣1,12).
(1)求此二次函数的解析式;
(2)该抛物线交x轴于点A,B(点A在点B的左侧),交y轴于点C,在抛物线对称轴上有一动点P,求PA+PC的最小值,并求当PA+PC取最小值时点P的坐标.
相关试题

