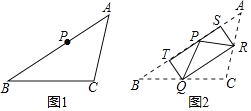
【题目】如图所示,图1为三角形纸片ABC,点P在AB上.若将纸片向内折叠,如图2所示,点A、B、C恰能重合在点P处,折痕分别为SR、RQ、QT,折痕的交点R、Q分别在边AC、BC上.若△ABC、四边形PTQR的面积分别是20和7,则△RPS的面积是_____.
【答案】3
【解析】
由折叠的性质得出△BTQ的面积和△PTQ的面积相等,△CQR和△PQR的面积相等,△ASR的面积和△PSR的面积相等,结合已知△ABC、四边形PTQR的面积分别,列式计算即可求解.
解:由折叠的性质得:△BTQ的面积和△PTQ的面积相等,△CQR和△PQR的面积相等,△ASR的面积和△PSR的面积相等.
又∵△ABC、四边形PTQR的面积分别为20和7,
∴△PRS面积等于(20﹣7×2)÷2=3.
故答案为:3.

