Question

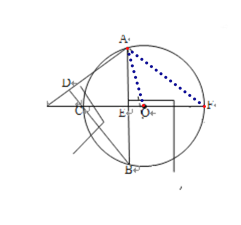
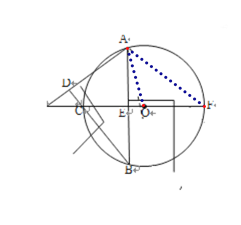
【题目】（本题8分）如图，⊙O是△ABC的外接圆，AD⊥BC于点D,直径CF⊥AB于点E,AD、FC的延长线交于点M。

(1)求证：EF=EM；

(2)若，AC=8，求sinM的值.

Answer 1

【答案】（1）答案见解析 （2）

（1）证明：连AF，∵∠DCE=∠B+∠CEB=∠M+CDM而AD⊥BC于点D，CF⊥AB于点E,∴∠CEB=∠CDM∴∠B=∠M,又∵∠B=∠F,∴∠M=∠F,∴AM=AF又∵EF=EM

（2）解：连AO,∵CF为直径，AB⊥CF于点E,∴AE=BE∴CA=CB,∠B=∠BAC,而∠AOE=2∠B,∠ACD=∠B+∠BAC=2∠B∴∠ACD=∠AOE,又∵AD⊥BD，AE⊥CF,∴∠ADC=∠AEO

△ADC∽△AEO,∴,而AC=8，∴CF=2AO=12

∵CF为直径,∴∠CAF=90°,∴在Rt△CAF中

AF= ==4,∴AM=4,易求

△OCA中AC上的高为2，用面积法求得AE=,sinM=

【解析】试题分析：本题考查了外角的性质，圆周角定理的推论，等腰三角形的判定与性质，垂径定理及其推论，相似三角形的判定与性质，勾股定理.

由三角形内角和得到∠B=∠M,由圆周角定理的推论可得∠B=∠F，从而∠M=∠F, △AMF是等腰三角形，由三线合一的性质可得EF=EM;

由垂径定理可得CA=CB,∠B=∠BAC,由圆周角定理的推论和外角性质可得∠ACD=∠AOE,进而证明△ADC∽△AEO,得到，求出CF的长，然后根据勾股定理求AF，面积法求AE，从而求sinM的值.

试题解析：

（1）证明：连AF，∵∠DCE=∠B+∠CEB=∠M+CDM而AD⊥BC于点D，CF⊥AB于点E,∴∠CEB=∠CDM∴∠B=∠M,又∵∠B=∠F,∴∠M=∠F,∴AM=AF又∵EF=EM

（2）解：连AO,∵CF为直径，AB⊥CF于点E,∴AE=BE∴CA=CB,∠B=∠BAC,而∠AOE=2∠B,∠ACD=∠B+∠BAC=2∠B∴∠ACD=∠AOE,又∵AD⊥BD，AE⊥CF,∴∠ADC=∠AEO

△ADC∽△AEO,∴,而AC=8，∴CF=2AO=12

∵CF为直径,∴∠CAF=90°,∴在Rt△CAF中

AF= ==4,∴AM=4,易求

△OCA中AC上的高为2，用面积法求得AE=,sinM=