【题目】如图,在平面直角坐标系中,已知△ABC的三个顶点的坐标分别为A(-3,5),B(-2,1),C(-1,3).
(1)若△ABC经过平移后得到△A1B1C1,已知点C1的坐标为(4,0),写出顶点A1,B1的坐标;
(2)若△ABC和△A2B2C2关于原点O成中心对称图形,写出△A2B2C2的各顶点的坐标;
(3)将△ABC绕着点O按顺时针方向旋转90°得到△A3B3C3,写出△A3B3C3的各顶点的坐标.

参考答案:
【答案】(1)点A1(2,2),点B1(3,-2).(2)A2(3,-5),B2(2,-1),C2(1,-3).(3)A3(5,3),B3(1,2),C3(3,1).
【解析】试题分析:(1)利用点C和点C1的坐标变化得到平移的方向与距离,然后利用此平移规律写出顶点A1,B1的坐标;
(2)根据关于原点对称的点的坐标特征求解;
(3)利用网格和旋转的性质画出△A2B3C3,然后写出△A2B3C3的各顶点的坐标.
解:(1)如图,△A1B1C1为所求三角形.因为点C(-1,3)平移后的对应点C1的坐标为(4,0),所以△ABC先向右平移5个单位,再向下平移3个单位得到△A1B1C1,所以点A1的坐标为(2,2),点B1的坐标为(3,-2).
(2)如图,因为△ABC和△A2B2C2关于原点O成中心对称图形,所以A2(3,-5),B2(2,-1),C2(1,-3).
(3)如图,△A3B3C3为所求三角形,A3(5,3),B3(1,2),C3(3,1).

-
科目: 来源: 题型:
查看答案和解析>>【题目】甲组有33个人,乙组有27个人,从乙组调若干人到甲组后,甲组的人数恰好是乙组的3倍,求变化后乙组有______人.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列命题:①如果两条直线都与第三条直线平行,那么这两条直线也互相平行;②内错角相等;③在同一平面内,如果两条直线都垂直于同一条直线,那么这两条直线平行;④相等的角是对顶角. 其中,真命题有( )
A.1个B.2个C.3个D.4个
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,两圆圆心相同,大圆的弦AB与小圆相切,AB=8,则图中阴影部分的面积是______.(结果保留π)

-
科目: 来源: 题型:
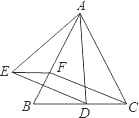
查看答案和解析>>【题目】如图,已知△ABC是等边三角形,点D、F分别在线段BC、AB上,∠EFB=60°,DC=EF.
(1)求证:四边形EFCD是平行四边形;
(2)若BF=EF,求证:AE=AD.
-
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙两个工程队计划修建一条长15千米的乡村公路,已知甲工程队每天比乙工程队每天多修路0.5千米,乙工程队单独完成修路任务所需天数是甲工程队单独完成修路任务所需天数的1.5倍.
(1)求甲、乙两个工程队每天各修路多少千米?
(2)若甲工程队每天的修路费用为0.5万元,乙工程队每天的修路费用为0.4万元,要使两个工程队修路总费用不超过5.2万元,甲工程队至少修路多少天?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知抛物线经过点A(-1,0)、B(3,0)、C(0,3)三点。
(1)求抛物线的解析式。
(2)点M是线段BC上的点(不与B,C重合),过M作MN∥y轴交抛物线于N若点M的横坐标为m,请用m的代数式表示MN的长。
(3)在(2)的条件下,连接NB、NC,是否存在m,使△BNC的面积最大?若存在,求m的值;若不存在,说明理由。

相关试题

