【题目】如图,已知D是△ABC中一边BC上的中点 ,AC∥BE,连接ED并延长ED交AC于点N,作DM⊥EN于点D交AB于点M.
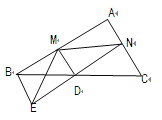
(1)求证:BE=CN
(2)试判断BM+CN与MN的大小关系,并说明理由.
参考答案:
【答案】(1)证明见解析;(2)BM+CN>MN.
【解析】
试题分析:(1)根据平行线的性质可证∠C=∠DBE,根据中点的定义可证BD=CD,根据AAS可证△BDE≌△CDN,根据全等三角形的性质可证DE=DN,BE=CN;
(2)根据DM⊥EN,可得∠MDE=∠MDN=90°,因为DE=DN,根据中垂线的性质可证ME=MN,根据三角形三边的关系可证BM+BE>ME,所以可证
试题解析:(1)∵AC//BE,BM+CN>MN.
∴∠C=∠DBE,
∵D是BC中点,
∴BD=CD,
又∠BDE=∠CDN,
∴△BDE≌△CDN(AAS),
∴DE=DN,BE=CN,
(2)∵DM⊥EN,
∴∠MDE=∠MDN=90°,
∵DE=DN,
∴ME=MN,
在△BME中BM+BE>ME,
又BE=CN,ME=MN,
∴BM+CN>MN.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某种速冻水饺的储藏温度是﹣18±2℃,四个冷藏室的温度如下,则不适合储藏此种水饺的是( )
A.﹣17℃
B.﹣22℃
C.﹣18℃
D.﹣19℃ -
科目: 来源: 题型:
查看答案和解析>>【题目】下列事件中,是随机事件的是( )
A. 通常加热到100℃时,水沸腾 B. 度量三角形的外角和,结果是360°
C. 明天太阳从西边升起 D. 篮球队员在罚球线上投篮一次,未投中
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列句子中不是命题的是( )
A. 两直线平行,同位角相等 B. 将4开平方
C. 若|a|=|b|,则a2=b2 D. 同角的补角相等
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知∠DAB+∠D=180°,AC平分∠DAB,且∠CAD=25°,∠B=95°
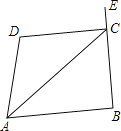
(1)、∠DCA的度数;
(2)、∠DCE的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】方程(x-2)2=3(x-2)的根是( )
A. 2 B. -2 C. 2或-2 D. 2或5
-
科目: 来源: 题型:
查看答案和解析>>【题目】命题“垂直于同一条直线的两条直线互相平行”的条件是( )
A. 垂直 B. 两条直线 C. 同一条直线 D. 两条直线垂直于同一条直线
相关试题

