【题目】相似三角形的判定定理:_______________的两个三角形相似;两边_________且夹角_______的两个三角形相似;三边__________的两个三角形相似.
参考答案:
【答案】 两角分别相等 成比例 相等 成比例
【解析】
根据相似三角形相似的判定定理,可知:两角对应相等的两三角形相似;
两边对应成比例且夹角相等的两三角形相似;三边对应成比例的两三角形相似.
相似三角形的判定定理:两角分别相等的两个三角形相似;两边对应成比例且夹角对应相等的两个三角形相似;三边对应成比例的两个三角形相似.
故答案为:两角分别相等;成比例;相等;成比例.
-
科目: 来源: 题型:
查看答案和解析>>【题目】因式分解:a2﹣3ab=__.
-
科目: 来源: 题型:
查看答案和解析>>【题目】先化简,再求值:(m﹣1)2﹣m(n﹣2)﹣(m﹣1)(m+1),其中m和n是面积为5的直角三角形的两直角边长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1~4,在直角边分别为3和4的直角三角形中,每多作一条斜边上的高就增加一个三角形的内切圆,依此类推,图10中有10个直角三角形的内切圆,它们的面积分别记为S1,S2,S3,…,S10,则S1+S2+S3+…+S10= .
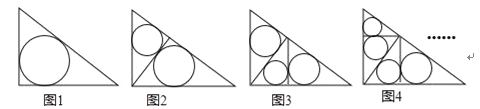
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知△ABC是等腰三角形,AB=AC.
(1)特殊情形:如图1,当DE∥BC时,有DB EC.(填“>”,“<”或“=”)
(2)发现探究:若将图1中的△ADE绕点A顺时针旋转α(0°<α<180°)到图2位置,则(1)中的结论还成立吗?若成立,请给予证明;若不成立,请说明理由.
(3)拓展运用:如图3,P是等腰直角三角形ABC内一点,∠ACB=90°,且PB=1,PC=2,PA=3,求∠BPC的度数.
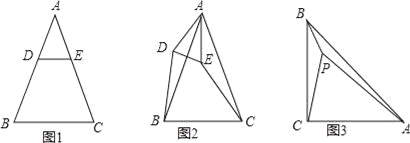
-
科目: 来源: 题型:
查看答案和解析>>【题目】图1是某公交公司1路车从起点站A站途经B站和C站,最终到达终点站D站的格点站路线图.(8×8的格点图是由边长为1的小正方形组成)
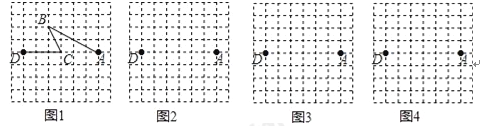
(1)求1路车从A站到D站所走的路程(精确到0.1);
(2)在图2、图3和图4的网格中各画出一种从A站到D站的路线图.(要求:①与图1路线不同、路程相同;②途中必须经过两个格点站;③所画路线图不重复)
-
科目: 来源: 题型:
查看答案和解析>>【题目】若(m+3)2+|n﹣2|=0,则﹣mn=_____
相关试题

