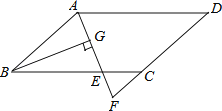
【题目】如图,在ABCD中,AB=6,AD=9,∠BAD的平分线交BC于点E,交DC的延长线于点F,BG⊥AE,垂足为G,BG=![]() ,则△CEF的周长为( )
,则△CEF的周长为( )
A.8 B.9.5 C.10 D.11.5
参考答案:
【答案】A
【解析】
试题分析:本题意在综合考查平行四边形、相似三角形、和勾股定理等知识的掌握程度和灵活运用能力,同时也体现了对数学中的数形结合思想的考查.在ABCD中,AB=CD=6,AD=BC=9,∠BAD的平分线交BC于点E,可得△ADF是等腰三角形,AD=DF=9;△ABE是等腰三角形,AB=BE=6,所以CF=3;在△ABG中,BG⊥AE,AB=6,BG=![]() ,可得AG=2,又△ADF是等腰三角形,BG⊥AE,所以AE=2AG=4,所以△ABE的周长等于16,又由ABCD可得△CEF∽△BEA,相似比为1:2,所以△CEF的周长为8,因此选A.
,可得AG=2,又△ADF是等腰三角形,BG⊥AE,所以AE=2AG=4,所以△ABE的周长等于16,又由ABCD可得△CEF∽△BEA,相似比为1:2,所以△CEF的周长为8,因此选A.
解:∵在ABCD中,AB=CD=6,AD=BC=9,∠BAD的平分线交BC于点E,
∴AB∥DC,∠BAF=∠DAF,
∴∠BAF=∠F,
∴∠DAF=∠F,
∴AD=FD,
∴△ADF是等腰三角形,
同理△ABE是等腰三角形,
AD=DF=9;
∵AB=BE=6,
∴CF=3;
∴在△ABG中,BG⊥AE,AB=6,BG=![]() ,可得:AG=2,
,可得:AG=2,
又BG⊥AE,
∴AE=2AG=4,
∴△ABE的周长等于16,
又∵ABCD
∴△CEF∽△BEA,相似比为1:2,
∴△CEF的周长为8.
故选:A.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知关于x的方程x2-(m+2)x+(2m-1)=0.
(1)求证:方程恒有两个不相等的实数根;
(2)若此方程的一个根是1,请求出方程的另一个根,并求出以此两根为边长的直角三角形的周长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】以下图形既是轴对称图形,又是中心对称图形的是( )
A.等腰三角形 B.平行四边形 C.矩形 D.等腰梯形
-
科目: 来源: 题型:
查看答案和解析>>【题目】等腰△ABC的直角边AB=BC=10cm,点P、Q分别从A、C两点同时出发,均以1cm/秒的相同速度作直线运动,已知P沿射线AB运动,Q沿边BC的延长线运动,PQ与直线AC相交于点D.设P点运动时间为t,△PCQ的面积为S.
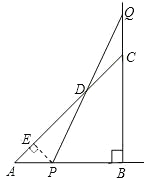
(1)求出S关于t的函数关系式;
(2)当点P运动几秒时,S△PCQ=S△ABC?
(3)作PE⊥AC于点E,当点P、Q运动时,线段DE的长度是否改变?证明你的结论.
-
科目: 来源: 题型:
查看答案和解析>>【题目】线段EF是由线段PQ平移得到的,点P(﹣1,4)的对应点为E(4,7),则点Q(﹣3,1)的对应点F的坐标为( )
A. (2,4) B. (﹣2,﹣2) C. (﹣8,﹣2) D. (﹣6,﹣1)
-
科目: 来源: 题型:
查看答案和解析>>【题目】当x=2时,函数y=kx+10与函数y=3x+3k的值相等,则k的值为( )
A. 2 B. 4 C. 6 D. 8
-
科目: 来源: 题型:
查看答案和解析>>【题目】根据相关部门统计,2014年我国共有9390000名学生参加高考,9390000用科学记数法表示为 .
相关试题

