【题目】问题探究:
1.新知学习
若把将一个平面图形分为面积相等的两个部分的直线叫做该平面图形的“面线”,其“面线”被该平面图形截得的线段叫做该平面图形的“面径”(例如圆的直径就是圆的“面径”).
2.解决问题

已知等边三角形ABC的边长为2.
(1)如图一,若AD⊥BC,垂足为D,试说明AD是△ABC的一条面径,并求AD的长;
(2)如图二,若ME∥BC,且ME是△ABC的一条面径,求面径ME的长;
(3)如图三,已知D为BC的中点,连接AD,M为AB上的一点(0<AM<1),E是DC上的一点,连接ME,ME与AD交于点O,且S△MOA=S△DOE.
①求证:ME是△ABC的面径;
②连接AE,求证:MD∥AE;
(4)请你猜测等边三角形ABC的面径长l的取值范围(直接写出结果)
参考答案:
【答案】(1)AD=![]() ;(2)ME=
;(2)ME=![]() ;(3)详见解析;(3)
;(3)详见解析;(3)![]() ≤l≤
≤l≤![]() .
.
【解析】
试题分析:(1)根据等腰三角形三线合一即可证明,利用直角三角形30°性质,即可求出AD.(2)根据相似三角形性质面积比等于相似比的平方,即可解决问题.(3)如图三中,作MN⊥AE于N,DF⊥AE于F,先证明MN=DF,推出四边形MNFD是平行四边形即可.
(4)如图四中,作MF⊥BC于F,设BM=x,BE=y,求出EM,利用不等式性质证明ME≥![]() 即可解决问题.
即可解决问题.
试题解析:(1)如图一中,

∵AB=AC=BC=2,AD⊥BC,
∴BD=DC,
∴S△ABD=S△ADC,
∴线段AD是△ABC的面径.
∵∠B=60°,
∴sin60°=![]() ,
,
∴![]() ,
,
∴AD=![]() .
.
(2)如图二中,
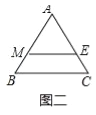
∵ME∥BC,且ME是△ABC的一条面径,
∴△AME∽△ABC,![]() =
=![]() ,
,
∴![]() ,
,
∴ME=![]() .
.
(3)如图三中,作MN⊥AE于N,DF⊥AE于F.
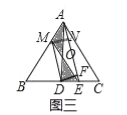
∵S△MOA=S△DOE,
∴S△AEM=S△AED,
∴![]() AEMN=
AEMN=![]() AEDF,
AEDF,
∴MN=DF,
∵MN∥DF,
∴四边形MNFD是平行四边形,
∴DM∥AE.
(4)如图四中,作MF⊥BC于F,设BM=x,BE=y,
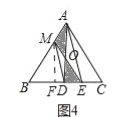
∵DM∥AE,
∴![]() ,
,
∴![]() ,
,
∴xy=2,
在RT△MBF中,∵∠MFB=90°,∠B=60°,BM=x,
∴BF=![]() x,MF=
x,MF=![]() x,
x,
∴ME=![]()
∴ME≥![]() ,
,
∵ME是等边三角形面径,AD也是等边三角形面积径,
∴等边三角形ABC的面径长l的取值范围![]() ≤l≤
≤l≤![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】小明为了了解本班全体同学在阅读方面的情况,采取全面调查的方法,从喜欢阅读“科普常识、小说、漫画、营养美食”等四类图书中调查了全班学生的阅读情况(要求每位学生只能选择一种自己喜欢阅读的图书类型)根据调查的结果绘制了下面两幅不完整的统计图.

请你根据图中提供的信息解答下列问题:
(1)该班喜欢阅读科普常识的同学有 人,该班的学生人数有 人;
(2)补全条形统计图;
(3)在扇形统计图中,表示“漫画”类所对圆心角是 度,喜欢阅读“营养美食”类图书的人数占全班人数的百分比为 .
-
科目: 来源: 题型:
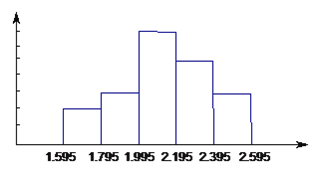
查看答案和解析>>【题目】某校七年级学生进行体育测试,七年级(2)班男生的立定跳远成绩制成频数分布直方图,图中从左到右各矩形的高之比是
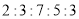 ,最后一组的频数是6,根据直方图所表达的信息,解答下列问题。
,最后一组的频数是6,根据直方图所表达的信息,解答下列问题。(1)该班有多少名男生?
(2)若立定跳远的成绩在2.0米以上(包括2.0米)为合格率是多少
-
科目: 来源: 题型:
查看答案和解析>>【题目】概念学习
规定:求若干个相同的有理数(均不等于0)的除法运算叫做除方,如2÷2÷2,
(﹣3)÷(﹣3)÷(﹣3)÷(﹣3)等.类比有理数的乘方,我们把2÷2÷2记作2③,读作“2的圈3次方”,(﹣3)÷(﹣3)÷(﹣3)÷(﹣3)记作(﹣3)④,读作“﹣3的圈4次方”,一般地,把
 (a≠0)记作a,读作“a的圈n次方”.
(a≠0)记作a,读作“a的圈n次方”.初步探究
(1)直接写出计算结果:2③=________,
 ⑤=________;
⑤=________;(2)关于除方,下列说法错误的是________
A.任何非零数的圈2次方都等于1; B.对于任何正整数n,1
 =1; C.3④=4③ D.负数的圈奇数次方结果是负数,负数的圈偶数次方结果是正数.
=1; C.3④=4③ D.负数的圈奇数次方结果是负数,负数的圈偶数次方结果是正数.深入思考
我们知道,有理数的减法运算可以转化为加法运算,除法运算可以转化为乘法运算,有理数的除方运算如何转化为乘方运算呢?

(1)试一试:仿照上面的算式,将下列运算结果直接写成幂的形式.(﹣3)④=________;5⑥=________;
 ⑩=________.
⑩=________.(2)想一想:将一个非零有理数a的圈n次方写成幂的形式等于________;
(3)算一算:
 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,矩形ABCD的顶点B,C在x轴上,A,D在第一象限,反比例函数y=
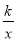 (x>0)的图象经过点A,交CD于点E,OB=2,AB=3.
(x>0)的图象经过点A,交CD于点E,OB=2,AB=3.(1)求k的值;
(2)若点E恰好是DC的中点.
①求直线AE的函数解析式;
②根据图象回答,在第一象限内,当x取何值时,反比例函数的函数值大于直线AE对应函数的函数值?
③若直线AE与x轴交于点M,与y轴交于点N,请你判断线段AN与线段ME的大小关系,并说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,在平面直角坐标系xOy中,抛物线y=ax2+1经过点A(4,﹣3),顶点为点B,点P为抛物线上的一个动点,l是过点(0,2)且垂直于y轴的直线,过P作PH⊥l,垂足为H,连接PO.
(1)求抛物线的解析式,并写出其顶点B的坐标;
(2)①当P点运动到A点处时,计算:PO= ,PH= ,由此发现,PO PH(填“>”、“<”或“=”);
②当P点在抛物线上运动时,猜想PO与PH有什么数量关系,并证明你的猜想;
(3)如图2,设点C(1,﹣2),问是否存在点P,使得以P,O,H为顶点的三角形与△ABC相似?若存在,求出P点的坐标;若不存在,请说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】点A(﹣3,2)与点B(﹣3,﹣2)的关系是( )
A. 关于x轴对称 B. 关于y轴对称 C. 关于原点对称 D. 以上各项都不对
相关试题

