【题目】如图,山坡上有一棵树AB,树底部B点到山脚C点的距离BC为6![]() 米,山坡的坡角为30°.小宁在山脚的平地F处测量这棵树的高,点C到测角仪EF的水平距离CF=1米,从E处测得树顶部A的仰角为45°,树底部B的仰角为20°,求树AB的高度.
米,山坡的坡角为30°.小宁在山脚的平地F处测量这棵树的高,点C到测角仪EF的水平距离CF=1米,从E处测得树顶部A的仰角为45°,树底部B的仰角为20°,求树AB的高度.
(参考数值:sin20°≈0.34,cos20°≈0.94,tan20°≈0.36)

参考答案:
【答案】6.4米
【解析】
试题分析:首先在直角三角形BDC中求得DC的长,然后求得DF的长,进而求得GF的长,然后在直角三角形BGE中即可求得BG的长,从而求得树高.
解:∵底部B点到山脚C点的距离BC为6![]() 米,山坡的坡角为30°.
米,山坡的坡角为30°.
∴在Rt△BDC中
DC=BCcos30°=6![]()
![]() =9米,
=9米,
∵CF=1米,
∴DF=9+1=10米,
∴GE=10米,
∵∠AEG=45°,
∴AG=EG=10米,
在直角三角形BGE中,
BG=GEtan20°=10×0.36=3.6米,
∴AB=AG﹣BG=10﹣3.6=6.4米,
答:树高约为6.4米.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB是⊙O的直径,经过圆上点D的直线CD恰使∠ADC=∠B.
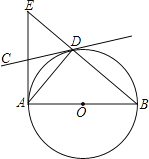
(1)求证:直线CD是⊙O的切线;
(2)过点A作直线AB的垂线交BD的延长线于点E,且AB=5,BD=2,求线段AE的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】方程x2=9的解为_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知⊙O1 和 ⊙O2相外切,O1 O2=7,⊙O1的半径为4,则⊙O2的半径为_________
-
科目: 来源: 题型:
查看答案和解析>>【题目】若等腰三角形底角为72°,则顶角为( )
A.108°
B.72°
C.54°
D.36° -
科目: 来源: 题型:
查看答案和解析>>【题目】有四根细木棒,长度分别为 3cm、5cm、7cm、9cm,以其中任意三条为边可以构成________个三角形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】有一人患了流感,经过两轮穿然后共有49人患了流感,设每轮传染中平均一个人传染了x人,则x的值为( )
A. 5 B. 6 C. 7 D. 8
相关试题

