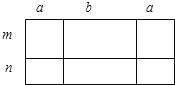
【题目】如图,甲、乙、丙、丁四位同学给出了四种表示该长方形面积的多项式:
①(2a+b)(m+n);②2a(m+n)+b(m+n);③m(2a+b)+n(2a+b);④2am+2an+bm+bn,你认为其中正确的有( )
A. ①② B. ③④ C. ①②③ D. ①②③④
参考答案:
【答案】D
【解析】①大长方形的长为2a+b,宽为m+n,利用长方形的面积公式,表示即可;
②长方形的面积等于左边,中间及右边的长方形面积之和,表示即可;
③长方形的面积等于上下两个长方形面积之和,表示即可;
④长方形的面积由6个长方形的面积之和,表示即可.
解答:解:①(2a+b)(m+n),本选项正确;
②2a(m+n)+b(m+n),本选项正确;
③m(2a+b)+n(2a+b),本选项正确;
④2am+2an+bm+bn,本选项正确,
则正确的有①②③④.
故选D.
“点睛”此题考查了多项式乘以多项式,熟练掌握运算法则是解本题的关键.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,在正方形ABCD中,E是AB上一点,F是AD延长线上一点,且DF=BE。
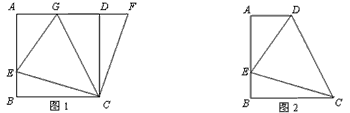
(1)求证:CE=CF;
(2)在图1中,若G在AD上,且∠GCE=45°,则GE=BE+GD成立吗?为什么?
(3)运用(1)(2)解答中所积累的经验和知识,完成下题:
如图2,在直角梯形ABCD中,AD∥BC(BC>AD),∠B=90°,AB=BC=12,E是AB上一点,且
∠DCE=45°,BE=4,求DE的长。 -
科目: 来源: 题型:
查看答案和解析>>【题目】将两张宽度相等的矩形纸片叠放在一起得到如图所示的四边形ABCD.

(1)求证:四边形ABCD是菱形;
(2)如果两张矩形纸片的长都是8,宽都是2.那么△DCB的面积是否存在最大值或最小值?如果存在,请求出来;如果不存在,请简要说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)计算:
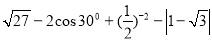 ;
;(2)解不等式:
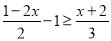 并将解集在数轴上表示出来.
并将解集在数轴上表示出来. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,AB=AD,∠1=∠2,以下条件中,不能推出△ABC≌△ADE的是( )

A. AE=AC B. ∠B=∠D C. BC=DE D. ∠C=∠E
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列计算正确的是( )
A. 2x2·4x2 =8x2 B. x5÷x-1=x4 C. (x4)4=x16 D. (-3x2)3=-9x6
-
科目: 来源: 题型:
查看答案和解析>>【题目】设4x2+mx+121是一个完全平方式,则m=________
相关试题

