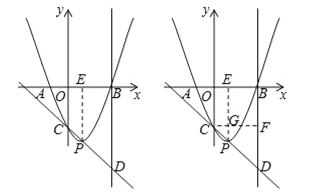
【题目】已知二次函数![]() (a>0)的图象与x轴的负半轴和正半轴分别交于A、B两点,与y轴交于点C,它的顶点为P,直线CP与过点B且垂直于x轴的直线交于点D,且CP:PD=2:3.
(a>0)的图象与x轴的负半轴和正半轴分别交于A、B两点,与y轴交于点C,它的顶点为P,直线CP与过点B且垂直于x轴的直线交于点D,且CP:PD=2:3.
(1)求A、B两点的坐标;
(2)若tan∠PDB=![]() ,求这个二次函数的关系式.
,求这个二次函数的关系式.
参考答案:
【答案】(1)A(![]() ,0);(2)
,0);(2)![]() .
.
【解析】
试题分析:(1)由二次函数的解析式可求出对称轴为x=1,过点P作PE⊥x轴于点E,所以OE:EB=CP:PD;
(2)过点C作CF⊥BD于点F,交PE于点G,构造直角三角形CDF,利用tan∠PDB=![]() 即可求出FD,由于△CPG∽△CDF,所以可求出PG的长度,进而求出a的值,最后将A(或B)的坐标代入解析式即可求出c的值.
即可求出FD,由于△CPG∽△CDF,所以可求出PG的长度,进而求出a的值,最后将A(或B)的坐标代入解析式即可求出c的值.
试题解析:(1)过点P作PE⊥x轴于点E,∵![]() ,∴该二次函数的对称轴为:x=1,∴OE=1
,∴该二次函数的对称轴为:x=1,∴OE=1
∵OC∥BD,∴CP:PD=OE:EB,∴OE:EB=2:3,∴EB=![]() ,∴OB=OE+EB=
,∴OB=OE+EB=![]() ,∴B(
,∴B(![]() ,0).
,0).
∵A与B关于直线x=1对称,∴A(![]() ,0);
,0);
(2)过点C作CF⊥BD于点F,交PE于点G,令x=1代入![]() ,∴y=c﹣a,令x=0代入
,∴y=c﹣a,令x=0代入![]() ,∴y=c,∴PG=a,∵CF=OB=
,∴y=c,∴PG=a,∵CF=OB=![]() ,∴tan∠PDB=
,∴tan∠PDB=![]() ,∴FD=2,∵PG∥BD,∴△CPG∽△CDF,∴
,∴FD=2,∵PG∥BD,∴△CPG∽△CDF,∴![]() ,∴PG=
,∴PG=![]() ,∴a=
,∴a=![]() ,∴
,∴![]() ,把A(
,把A(![]() ,0)代入
,0)代入![]() ,∴解得:c=﹣1,∴该二次函数解析式为:
,∴解得:c=﹣1,∴该二次函数解析式为:![]() .
.
-
科目: 来源: 题型:
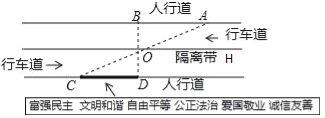
查看答案和解析>>【题目】杨阳同学沿一段笔直的人行道行走,在由A步行到达B处的过程中,通过隔离带的空隙O,刚好浏览完对面人行道宣传墙上的社会主义核心价值观标语,其具体信息汇集如下:
如图,AB∥OH∥CD,相邻两平行线间的距离相等,AC,BD相交于O,OD⊥CD.垂足为D,已知AB=20米,请根据上述信息求标语CD的长度.
-
科目: 来源: 题型:
查看答案和解析>>【题目】若m2-2m=-3则8-2m2+4m的值为_________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】化简
(1)3a2+5b-2a2-2a+3a-8b (2)3(2x-5y)-4(3x-5y)+5
-
科目: 来源: 题型:
查看答案和解析>>【题目】地球绕太阳公转的速度约是110000千米/时,将110000用科学记数法表示为( )
A.11×104
B.1.1×105
C.1.1×104
D.0.11×105 -
科目: 来源: 题型:
查看答案和解析>>【题目】下列计算正确的是( )
A.x4x4=x16
B.(a3)2=a5
C.(ab2)3=ab6
D.a+2a=3a -
科目: 来源: 题型:
查看答案和解析>>【题目】如图:在△ABC中,BE、CF分别是AC、AB两边上的高,在BE上截取BD=AC,在CF的延长线上截取CG=AB,连结AD、AG。
(1)求证:AD=AG
(2)AD与AG的位置关系如何,请说明理由。

相关试题

