搜索
【题目】已知函数y＝
（n为常数）．
（1）当n＝1时，
①点P（﹣3，m）在此函数图象上，求m的值．
②当﹣4≤x≤3时，求此函数的最大值和最小值．
（2）当x＜n时，若此函数的图象与坐标轴只有两个交点，求n的取值范围．
（3）若n＞0，当此函数的图象与以A（0，3）、B（5，﹣2）、C（﹣5，﹣2）、D（﹣5，3）为顶点的四边形的边有且只有四个公共点时，直接写出n的取值范围．
【答案】（1）①-1；②最大值为5，最小值为﹣6；（2）0＜n≤
；（3）1＜n≤
或2.6＜n＜2.9．
【解析】
（1）①利用待定系数法解决问题即可．
②分别求出分段函数在-4≤x≤3上的最大值以及最小值即可解决问题．
（2）分n＞0，n=0，n＜0三种情形画出图形分别求解即可．
（3）分两种情形：如图3-1中，当四边形ABCD与函数y=-x2-2nx+2（x＜n）有3个交点，与函数y=x2-2nx+2（x≥n）有1个交点时，如图3-2中，当四边形ABCD与函数y=-x2-2nx+2（x＜n）有2个交点，与函数y=x2-2nx+2（x≥n）有2个交点时，
分别构建不等式组解决问题即可．
（1）n＝1时，函数为y＝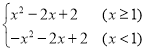
，
①∵P（﹣3，m）在函数图象上，
∴m＝﹣9+6+2＝﹣1．
②当﹣4≤x＜1时，y＝﹣x2﹣2x+2，最小值为﹣16+8+2＝﹣6，最大值为﹣1+2+2＝3，
当1＜x≤3时，y＝x2﹣2x+2，最小值为1﹣2+2＝1，最大值为9﹣6+2＝5，
综上所述，当﹣4≤x≤3时，此函数的最大值为5，最小值为﹣6．
（2）①当n＞0时，图象如图所示，
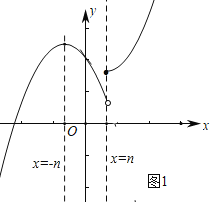
当函数y＝﹣x2﹣2nx+2，x＝n时，y≥0即可满足条件，
∴﹣n2﹣2n2+2≥0，
解得﹣≤n≤，
∵n＞0，
∴0＜n≤．
②当n＝0时，显然不符合题意．
③当n＜0时，不存在符合条件的n的值．
综上所述，满足条件的n的值为0＜n≤．
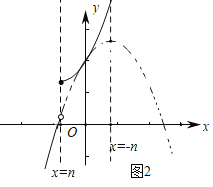
（3）如图3﹣1中，当四边形ABCD与函数y＝﹣x2﹣2nx+2（x＜n）有3个交点，与函数y＝x2﹣2nx+2（x≥n）有1个交点时，
满足：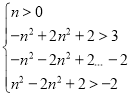
，
解得1＜n≤．
如图3﹣2中，当四边形ABCD与函数y＝﹣x2﹣2nx+2（x＜n）有2个交点，与函数y＝x2﹣2nx+2（x≥n）有2个交点时，
满足：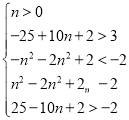
，
解得2.6＜n＜2.9．
综上所述，满足条件的n的值为1＜n≤或2.6＜n＜2.9．
