【题目】如图,△ABC中,AB=AC,以边AB为直径作⊙O,交BC于点D,过D作DE⊥AC于点E.
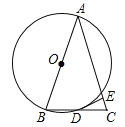
(1)求证:DE为⊙O的切线;
(2)若AB=13,sinB=![]() ,求DE的长.
,求DE的长.
参考答案:
【答案】(1)证明见试题解析;(2)![]() .
.
【解析】试题分析:(1)连接OD,利用平行线的判定定理可以得到∠ODE=∠DEC=90°,从而判断DE是圆的切线;
(2)根据AB=13,sinB=![]() ,可求得AD和BD,再由∠B=∠C,即可得出DE的长.
,可求得AD和BD,再由∠B=∠C,即可得出DE的长.
试题解析:(1)证明:连接OD,

∵O、D分别是AB、BC的中点,
∴OD∥AC,
∴∠ODE=∠DEC=90°,
∴OD⊥DE,
∴DE是⊙O的切线;
(2)解:∵AB=13,sinB=![]() ,
,
∴![]() ,
,
∴AD=12,
∴由勾股定理得BD=5,
∴CD=5,
∵∠B=∠C,
∴![]() ,
,
∴DE=![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】若3﹣2a>3﹣2b,则ab(填“>”“<”或“=”).
-
科目: 来源: 题型:
查看答案和解析>>【题目】将点A(3,2)沿x轴向左平移4个单位长度得到点A′,点A′关于y轴对称的点的坐标是( )
A. (﹣3,2) B. (﹣1,2) C. (1,2) D. (1,﹣2)
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知a,b互为相反数,c,d互为倒数,|e|=
 ,则代数式5(a+b)2+
,则代数式5(a+b)2+  cd﹣2e的值为( )
cd﹣2e的值为( )
A.﹣
B.
C. 或﹣
或﹣ 
D.﹣ 或
或 
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,某小区有一块长为30m,宽为24m的矩形空地,计划在其中修建两块相同的矩形绿地,它们的面积之和为480m2,两块绿地之间及周边有宽度相等的人行通道,则人行通道的宽度为多少米.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,抛物线y=ax2+bx+
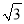 与x轴交于A(-3,0),B(1,0)两点,与y轴交于点C,点D与点C关于抛物线的对称轴对称.
与x轴交于A(-3,0),B(1,0)两点,与y轴交于点C,点D与点C关于抛物线的对称轴对称.(1)求抛物线的解析式,并直接写出点D的坐标;
(2)如图1,点P从点A出发,以每秒1个单位长度的速度沿A→B匀速运动,到达点B时停止运动.以AP为边作等边△APQ(点Q在x轴上方).设点P在运动过程中,△APQ与四边形AOCD重叠部分的面积为S,点P的运动时间为t秒,求S与t之间的函数关系式;
(3)如图2,连接AC,在第二象限内存在点M,使得以M、O、A为顶点的三角形与△AOC相似.请直接写出所有符合条件的点M坐标.

-
科目: 来源: 题型:
查看答案和解析>>【题目】若点A(2,a)关于x轴的对称点是B(b,﹣3),则ab的值是 .
相关试题

