Question

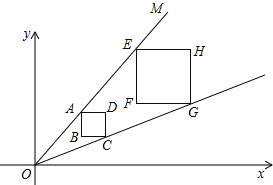
【题目】已知在平面直角坐标系中，点O为坐标原点，过O的直线OM经过点A（6，6），过A作正方形ABCD，在直线OA上有一点E，过E作正方形EFGH，已知直线OC经过点G，且正方形ABCD的边长为2，正方形EFGH的边长为3，则点F的坐标为 ．

Answer 1

【答案】（9，6）．

【解析】

试题分析：先利用待定系数法确定直线OA的解析式为y=mx，根据坐标与图形变换由点A（6，6），正方形ABCD的边长为2得到D点坐标为（8，6），C点坐标为（8，4），再利用待定系数法确定直线OC的解析式为y=x，则可设G点坐标为（t，t），由于正方形EFGH的边长为3，所以H点坐标为（t，t+3），从而得到E点坐标为（t﹣3，t+3），然后把把E点坐标代入y=x求出t=12，得到E点坐标为（9，9），再把E点向下平移3个单位即可得到F点的坐标．

解：设直线OA的解析式为y=mx，

把A（6，6）代入得6m=6，解得m=1，

∴直线OA的解析式为y=x，

∵点A（6，6），正方形ABCD的边长为2，

∴D点坐标为（8，6），C点坐标为（8，4）．

设直线OC的解析式为y=kx，

把C（8，4）代入y=kx

得8k=4，解得k=，

∴直线OC的解析式为y=x，

设G点坐标为（t，t），

∵正方形EFGH的边长为3，

∴H点坐标为（t，t+3），E点坐标为（t﹣3，t+3），

把E（t﹣3，t+3）代入y=x

得t﹣3=t+3，解得t=12，

∴E点坐标为（9，9），

∴F点的坐标为（9，6）．

故答案为：（9，6）．