搜索
【题目】如图为等边△ABC与正方形DEFG的重叠情形，其中D、E两点分别在AB、BC上，且BD=BE，若AB=3，DE=1，则△EFC的面积为（ ） 
A.
B.1
C.
D.
参考答案：
【答案】D
【解析】解：如图，作FM⊥BC于M， ∵△ABC是等边三角形，
∴∠B=60°，BC=AB=3，
∵BD=BE，
∴△BDE是等边三角形，
∴∠BED=60°，
∵四边形DEFG是正方形，EF=DE=1，∠DEF=90°，
∴∠FEM=30°，
∴FM= 
EF= ，
∵EC=BC﹣BE=2，
∴△EFC的面积= ×2× = ．
故选：D．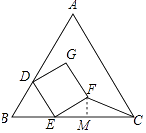
【考点精析】本题主要考查了三角形的面积和等边三角形的性质的相关知识点，需要掌握三角形的面积=1/2×底×高；等边三角形的三个角都相等并且每个角都是60°才能正确解答此题．
-
科目： 来源： 题型：
查看答案和解析>>【题目】小明的爸爸和妈妈分别驾车从家同时出发去上班，爸爸行驶到甲处时，看到前面路口时红灯，他立即刹车减速并在乙处停车等待，爸爸驾车从家到乙处的过程中，速度v（m/s）与时间t（s）的关系如图1中的实线所示，行驶路程s（m）与时间t（s）的关系如图2所示，在加速过程中，s与t满足表达式s=at2
（1）根据图中的信息，写出小明家到乙处的路程，并求a的值；
（2）求图2中A点的纵坐标h，并说明它的实际意义；
（3）爸爸在乙处等代理7秒后绿灯亮起继续前行，为了节约能源，减少刹车，妈妈驾车从家出发的行驶过程中，速度v（m/s）与时间t（s）的关系如图1中的折线O﹣B﹣C所示，行驶路程s（m）与时间t（s）的关系也满足
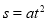，当她行驶到甲处时，前方的绿灯刚好亮起，求此时妈妈驾车的行驶速度．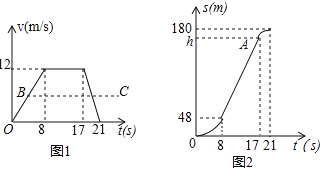
-
科目： 来源： 题型：
查看答案和解析>>【题目】若2a﹣3b2=5，则6﹣2a+3b2= ．
-
科目： 来源： 题型：
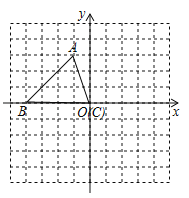
查看答案和解析>>【题目】如图，平面直角坐标系内，小正方形网格的边长为1个单位长度，△ABC的三个顶点的坐标分别为A（﹣1，3），B（﹣4，0），C（0，0）
（1）画出将△ABC向上平移1个单位长度，再向右平移5个单位长度后得到的△A1B1C1；
（2）画出将△ABC绕原点O顺时针方向旋转90°得到△A2B2O；
（3）在x轴上存在一点P，满足点P到A1与点A2距离之和最小，请直接写出P点的坐标．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，已知数轴上点A表示的数为﹣7，点B表示的数为5，点C到点A，点B的距离相等，动点P从点A出发，以每秒2个单位长度的速度沿数轴向右匀速运动，设运动的时间为t（t＞0）秒．
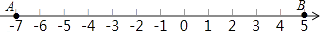
（1）点C表示的数是；
（2）求当t等于多少秒时，点P到达点B处；
（3）点P表示的数是（用含有t的代数式表示）；
（4）求当t等于多少秒时，PC之间的距离为2个单位长度． -
科目： 来源： 题型：
查看答案和解析>>【题目】如图，△ABC三个顶点的坐标分别为A（1，1），B（4，2），C（3，4）．
（1）请画出将△ABC向左平移4个单位长度后得到的图形△A1B1C1；
（2）请画出△ABC关于原点O成中心对称的图形△A2B2C2；
（3）在x轴上找一点P，使PA+PB的值最小，请直接写出点P的坐标．
-
科目： 来源： 题型：
查看答案和解析>>【题目】已知a、b、c满足|a﹣
|+ 
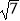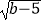+（c﹣4 
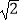）2=0．
（1）求a、b、c的值；
（2）判断以a、b、c为边能否构成三角形？若能构成三角形，此三角形是什么形状？并求出三角形的面积；若不能，请说明理由．
相关试题
