【题目】如图，抛物线与轴交于、两点，与轴交于点．直线经过点、．

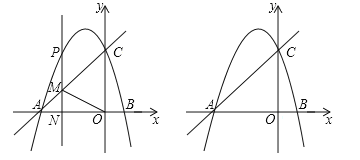
（1）求抛物线的解析式；

（2）是抛物线上一动点，过作轴交直线于点，设点的横坐标为．

①若以点、、、为顶点的四边形是平行四边形，求的值．

②当射线、、中一条射线平分另外两条射线的夹角时，直接写出的值．

【答案】（1）；（2）①的值为或或；②或．

【解析】

（1）先根据直线解析式求出A、C两点的坐标，把点A和C点的坐标代入得关于b和c的方程组，然后解方程组即可得到抛物线解析式；

（2）当OC∥PM，且OC＝PM时，以点C、O、M、P为顶点的四边形是平行四边形，可得关于t的方程，解方程即可；

（3）分两种情况考虑，当AC平分MP、MO的夹角，当MO平分AC、MP的夹角，可由图形的性质得关于t的方程求解．

解：（1）在中，令x＝0，y＝3；令y＝0，x＝4，得A（4，0），C（0，3），

∵抛物线过点、，

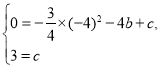∴，解得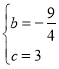

∴抛物线的解析式为．

（2）①设点，

∵四边形OCMP为平行四边形，

∴PM＝OC＝3，PM∥OC，

∴M点的坐标可表示为，则．

∴，

当＝3，解得t＝2，

当＝3，解得，，

即的值为或或．

②如图1，若AC平分MP、MO的夹角，过点C作CH⊥OA，CG⊥MP，

则CG＝CH，

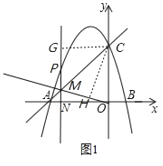
∵S△MCO＝OMCH＝OCCG，

∴OM＝OC＝3，

∵点M在直线AC上，

∴M（t，t＋3），

∴MN2＋ON2＝OM2，可得，t2＋(t＋3)2＝9，

解得t＝，

如图2，若MO平分AC、MP的夹角，则可得∠NMO＝∠OMC，过点O作OK⊥AC，

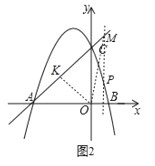
∴OK＝ON，

∵∠AKO＝∠AOC＝90，∠OAK＝OAC，

∴△AOK∽△ACO，

∴，

∴，

∴OK＝，

由角平分线的性质可得：点O到AC和MP的距离相等，

∴t＝，

综合以上可得t的值为或．

关闭