【题目】如图,⊙O是△ABC的外接圆,AB是⊙O的直径,经过点A作AE⊥OC,垂足为点D,AE与BC交于点F,与过点B的直线交于点E,且EB=EF.
(1)求证:BE是⊙O的切线;
(2)若CD=1,cos∠AEB=![]() ,求BE的长.
,求BE的长.

参考答案:
【答案】(1)见解析;(2)BE=![]()
【解析】
(1)由OB=OC可得∠OBC=∠OCB,由EB=EF可知∠EBC=∠EFB,根据∠AFC+∠OCB=90°可知∠EBC+∠OBC=90°,即可得结论;
(2)由(1)可知∠AEB+∠EAB=90°,由∠AOD+∠EAB=90°即可证明∠AOD=∠AEB,设⊙O的半径为r,根据cos∠AOD=cos∠AEB=![]() 可求出r的值,即可得AB的值,根据cos∠AEB=
可求出r的值,即可得AB的值,根据cos∠AEB=![]() =
=![]() 可得AE=
可得AE=![]() BE,利用勾股定理求出BE的长即可.
BE,利用勾股定理求出BE的长即可.
(1)∵B、C在⊙O上,
∴OB=OC,
∴∠OBC=∠OCB,
∵EF=EB,
∴∠EBC=∠EFB,
又∵∠AFC=∠EFB,
∴∠AFC=∠EBC,
∵AE⊥OC,
∴∠AFC+∠OCB=90°,
∴∠EBC+∠OBC=90°,即BE⊥OB,
又OB是⊙O的半径,
∴EB是⊙O的切线;
(2)设⊙O的半径为r,则OA=OC=r,
又CD=1,
∴OD=r﹣1,
∵∠AOD+∠EAB=90°,∠AEB+∠EAB=90°,
∴∠AOD=∠AEB,
∴cos∠AOD=cos∠AEB=![]() ,
,
∴在Rt△AOD中,cos∠AOD=![]() =
=![]() ,即
,即![]() =
=![]() ,
,
解得:r=![]() ,
,
∵AB是⊙O的直径,
∴AB=5,
在Rt△AEB中,cos∠AEB=![]() =
=![]() ,
,
∴AE=![]() BE,
BE,
又AE2=AB2+BE2,即(![]() BE)2=BE2+52,
BE)2=BE2+52,
解得:BE=![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线AB和抛物线的交点是A(0,-3),B(5,9),已知抛物线的顶点D的横坐标是2.

(1)求抛物线的解析式及顶点坐标;
(2)在
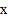 轴上是否存在一点C,与A,B组成等腰三角形?若存在,求出点C的坐标,若不存在,请说明理由;
轴上是否存在一点C,与A,B组成等腰三角形?若存在,求出点C的坐标,若不存在,请说明理由;(3)在直线AB的下方抛物线上找一点P,连接PA,PB使得△PAB的面积最大,并求出这个最大值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,字母S由两条圆弧KL、MN和线段LM组成,这两条圆弧每一条都是一个半径为1的圆的圆周的
 ,线段LM与两个圆相切.K和N分别是两个圆的切点,则线段LM的长为_________.
,线段LM与两个圆相切.K和N分别是两个圆的切点,则线段LM的长为_________.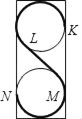
-
科目: 来源: 题型:
查看答案和解析>>【题目】问题:如图(1),点E、F分别在正方形ABCD的边BC、CD上,∠EAF=45°,试判断BE、EF、FD之间的数量关系.
【发现证明】小聪把△ABE绕点A逆时针旋转90°至△ADG,从而发现EF=BE+FD,请你利用图(1)证明上述结论.
【类比引申】如图(2),四边形ABCD中,∠BAD≠90°,AB=AD,∠B+∠D=180°,点E、F分别在边BC、CD上,则当∠EAF与∠BAD满足 关系时,仍有EF=BE+FD;请证明你的结论.

【探究应用】如图(3),在某公园的同一水平面上,四条通道围成四边形ABCD.已知AB=AD=80米,∠B=60°,∠ADC=120°,∠BAD=150°,道路BC、CD上分别有景点E、F,且AE⊥AD,DF=40(
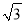 ﹣1)米,现要在E、F之间修一条笔直道路,求这条道路EF的长.(结果取整数,参考数据:
﹣1)米,现要在E、F之间修一条笔直道路,求这条道路EF的长.(结果取整数,参考数据: 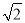 =1.41,
=1.41,  =1.73)
=1.73) -
科目: 来源: 题型:
查看答案和解析>>【题目】“端午节”是我国的传统佳节,民间历来有吃“粽子”的习俗.我市某食品厂为了解市民对去年销量较好的肉馅粽、豆沙馅粽、红枣馅粽、蛋黄馅粽(以下分别用A、B、C、D表示)这四种不同口味粽子的喜爱情况,在节前对某居民区市民进行了抽样调查,并将调查情况绘制成如下两幅统计图(尚不完整).

请根据以上信息回答:
(1)本次参加抽样调查的居民有多少人?
(2)将两幅不完整的图补充完整;
(3)求扇形统计图中C所对圆心角的度数;
(4)若有外型完全相同的A、B、C、D粽各一个,煮熟后,小王吃了两个.用列表或画树状图的方法,求他第二个吃到的恰好是C粽的概率.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图是某货站传送货物的平面示意图.为了提高传送过程的安全性,工人师傅欲减小传送带与地面的夹角,使其由45°改为30°.已知原传送带AB长为4
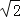 米.
米.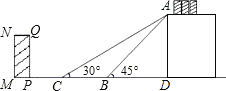
(1)求新传送带AC的长度.
(2)如果需要在货物着地点C的左侧留出2米的通道,试判断距离B点5米的货物MNQP是否需要挪走,并说明理由.
参考数据:
 .
. -
科目: 来源: 题型:
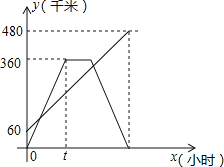
查看答案和解析>>【题目】甲、乙两车分别从相距480km的A、B两地相向而行,乙车比甲车先出发1小时,并以各自的速度匀速行驶,途径C地,甲车到达C地停留1小时,因有事按原路原速返回A地.乙车从B地直达A地,两车同时到达A地.甲、乙两车距各自出发地的路程y(千米)与甲车出发所用的时间x(小时)的关系如图,结合图象信息解答下列问题:
(1)乙车的速度是 千米/时,t= 小时;
(2)求甲车距它出发地的路程y与它出发的时间x的函数关系式,并写出自变量的取值范围;
(3)直接写出乙车出发多长时间两车相距120千米.
相关试题

