搜索
【题目】下列命题是真命题的是（ ）
A. 对角线相等的平行四边形是矩形
B. 菱形的对角线相等
C. 四边都相等的四边形是矩形
D. 对角线互相垂直的平行四边形是正方形
参考答案：
【答案】A
【解析】
据矩形的判定定理、菱形的性质定理、正方形的判定定理判断即可．
解：A、对角线相等的平行四边形是矩形，A是真命题；
B、菱形的对角线互相垂直，B是假命题；
C、四边都相等的平行四边形是矩形，C是假命题；
D、对角线互相垂直且相等的平行四边形是正方形，D是假命题；
故选：A．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在△ABC中，∠B=55°，∠C=30°．
（1）请用尺规作AC的垂直平分线MN，交BC于点D，连接AD，（保留作图痕迹，不写作法）
（2）求∠BAD的度数． -
科目： 来源： 题型：
查看答案和解析>>【题目】某农资公司购进甲、乙两种农药，乙种农药的单价是甲种农药单价的3倍，购买250元甲种农药的数量比购买300元乙种农药的数量多15，求两种农药单价各为多少元？
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在△ABC中，AB=AC，以AB为直径作半圆⊙O，交BC于点D，连接AD、过点D作DE⊥AC，垂足为点E，交AB的延长线于点F．
（1）求证：EF是⊙O的切线；
（2）求证：△FDB∽△FAD；
（3）如果⊙O的半径为5，sin∠ADE=
，求BF的长．
-
科目： 来源： 题型：
查看答案和解析>>【题目】阅读理解：运用“同一图形的面积相等”可以证明一些含有线段的等式成立，这种解决问题的方法我们称之为面积法. 如图1，在等腰△ABC中，AB=AC， AC边上的高为h，点M为底边BC上的任意一点，点M到腰AB、AC的距离分别为h1、h2，连接AM，利用S△ABC=S△ABM＋S△ACM，可以得出结论：h= h1＋h2.
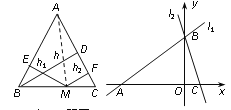
类比探究：在图1中，当点M在BC的延长线上时，猜想h、h1、h2之间的数量关系并证明你的结论.
拓展应用：如图2，在平面直角坐标系中，有两条直线l1：y =
x+3，l2：y =－3x+3，若l2上一点M到l1的距离是1，试运用 “阅读理解”和“类比探究”中获得的结论，求出点M的坐标. -
科目： 来源： 题型：
查看答案和解析>>【题目】某次数学测验，共有16道选择题，评分方法是：答对一题得6分，不答或答错一题扣2分．某同学要想得分为60分以上，他至少应答对多少道题?(只列关系式)
-
科目： 来源： 题型：
查看答案和解析>>【题目】下列事件中，属于随机事件的是（ ）
A. 科学实验，前500次实验都失败了，第501次实验会成功
B. 投掷一枚骰子，朝上面出现的点数是7点
C. 天空出现两个太阳
D. 用长度分别是6cm，8cm，10cm的细木条首尾顺次相连可组成一个直角三角形
相关试题
