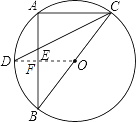
【题目】如图.Rt△ABC内接于⊙O,BC为直径,AB=4,AC=3,D是弧AB 的中点,CD与AB的交点为E,则![]() 等于( )
等于( )

A. 4 B. 3.5 C. 3 D. 2.8
参考答案:
【答案】C
【解析】如图,连接DO,交AB于点F,由垂径定理的知识可得出DO⊥AB,AF=BF,进而得出DF的长和△DEF∽△CEA,再利用相似三角形的性质求出即可.
如图,连接DO,交AB于点F,
∵D是![]() 的中点,
的中点,
∴DO⊥AB,AF=BF,
∵AB=4,
∴AF=BF=2,
∴FO是△ABC的中位线,AC∥DO,
∵BC为直径,AB=4,AC=3,
∴BC=5,FO=![]() AC=1.5,
AC=1.5,
∴DO=2.5,
∴DF=2.5﹣1.5=1,
∵AC∥DO,
∴△DEF∽△CEA,
∴![]() ,
,
∴ ![]() =3,
=3,
故选C.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(知识生成)
我们已经知道,通过不同的方法表示同一图形的面积,可以探求相应的等式.
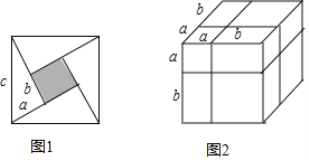
2002年8月在北京召开了国际数学大会,大会会标如图1所示,它是由四个形状大小完全相同的直角三角形与中间的小正方形拼成的一个大正方形,直角三角形的两条直角边长分别为a、b ( a<b ),斜边长为c.
(1)图中阴影部分的面积用两种方法可分别表示为 、 ;
(2)你能得出的a,b,c之间的数量关系是 (等号两边需化为最简形式);
(3)一直角三角形的两条直角边长为6和8,则其斜边长为 .
(知识迁移)
通过不同的方法表示同一几何体的体积,也可以探求相应的等式.如图2是边长为a+b的正方体,被如图所示的分割线分成8块.
(4)用不同方法计算这个正方体体积,就可以得到一个等式,这个等式可以为 .(等号两边需化为最简形式)
(5)已知a+b=3,ab=1,利用上面的规律求a3+b3的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,等腰三角形ABC的底边BC长为4,面积是16,腰AC的垂直平分线EF分别交AC,AB边于E,F点
 若点D为BC边的中点,点M为线段EF上一动点,则
若点D为BC边的中点,点M为线段EF上一动点,则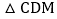 周长的最小值为
周长的最小值为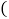

A. 6 B. 8 C. 10 D. 12
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,抛物线y=ax2+2x+c与x轴交于A(﹣1,0)B(3,0)两点,与y轴交于点C,点D是该抛物线的顶点.
(1)求抛物线的解析式和直线AC的解析式;
(2)请在y轴上找一点M,使△BDM的周长最小,求出点M的坐标;
(3)试探究:在拋物线上是否存在点P,使以点A,P,C为顶点,AC为直角边的三角形是直角三角形?若存在,请求出符合条件的点P的坐标;若不存在,请说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知关于x的一次函数y=mx+2的图象经过点(﹣2,6).
(1)求m的值;
(2)画出此函数的图象;
(3)平移此函数的图象,使得它与两坐标轴所围成的图形的面积为4,请直接写出此时图象所对应的函数关系式.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:点C在直线AB上,AC=8cm,BC=6cm,点M、N分别是AC、BC的中点,求线段MN的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,OA的方向是北偏东15°,OB的方向是西偏北50度.
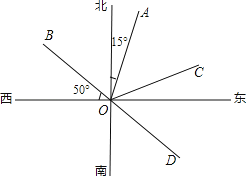
(1)若∠AOC=∠AOB,则OC的方向是 ;
(2)OD是OB的反向延长线,OD的方向是 ;
(3)∠BOD可看作是OB绕点O逆时针方向至OD,作∠BOD的平分线OE,OE的方向是 ;
(4)在(1)、(2)、(3)的条件下,∠COE= .
相关试题

