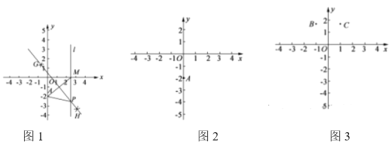
【题目】如图1,在平面直角坐标系中,点A的坐标是![]() ,在x轴上任取一点M.连接AM,分别以点A和点M为圆心,大于
,在x轴上任取一点M.连接AM,分别以点A和点M为圆心,大于![]() 的长为半径作弧,两弧相交于G,H两点,作直线GH,过点M作x轴的垂线l交直线GH于点P.根据以上操作,完成下列问题.
的长为半径作弧,两弧相交于G,H两点,作直线GH,过点M作x轴的垂线l交直线GH于点P.根据以上操作,完成下列问题.
探究:
(1)线段PA与PM的数量关系为________,其理由为:________________.
(2)在x轴上多次改变点M的位置,按上述作图方法得到相应点P的坐标,并完成下列表格:
M的坐标 | … |
|
|
|
| … |
P的坐标 | … |
|
| … |
猜想:
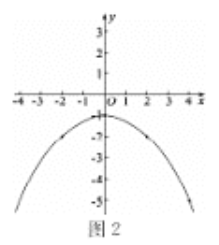
(3)请根据上述表格中P点的坐标,把这些点用平滑的曲线在图2中连接起来;观察画出的曲线L,猜想曲线L的形状是________.
验证:
(4)设点P的坐标是![]() ,根据图1中线段PA与PM的关系,求出y关于x的函数解析式.
,根据图1中线段PA与PM的关系,求出y关于x的函数解析式.
应用:
(5)如图3,点![]() ,
,![]() ,求点D的纵坐标
,求点D的纵坐标![]() 的取值范围.
的取值范围.
【答案】(1)![]() ,线段垂直平分线上的点与这条线段两个端点的距离相等;(2)图见解析,抛物线;(3)见解析;(4)
,线段垂直平分线上的点与这条线段两个端点的距离相等;(2)图见解析,抛物线;(3)见解析;(4)![]() ;(5)
;(5)![]()
【解析】
(1)由尺规作图的步骤可知,HG是AM的中垂线,结合中垂线的性质,即可得到答案;
(2)根据第(1)的作图方法,得到相应点P的位置,即可求解;
(3)用平滑的曲线作出图象,即可;
(4)过点P作![]() 轴于点E,用含x,y的代数式表示
轴于点E,用含x,y的代数式表示![]() ,
,![]() ,
,![]() ,结合勾股定理,即可得到答案;
,结合勾股定理,即可得到答案;
(5)连接![]() ,由题意得当
,由题意得当![]() 时,在
时,在![]() 的外接圆上,弧
的外接圆上,弧![]() 所对的圆心角为60°,
所对的圆心角为60°,![]() 的外接圆圆心为坐标原点O,设
的外接圆圆心为坐标原点O,设![]() ,求出b的值,进而即可求解.
,求出b的值,进而即可求解.
解:(1)![]() 线段垂直平分线上的点与这条线段两个端点的距离相等
线段垂直平分线上的点与这条线段两个端点的距离相等
(2)
M的坐标 | … |
|
|
|
| … |
P的坐标 | … |
|
|
|
| … |
(3)草图见图2:形状:抛物线
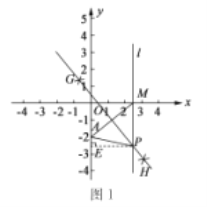
(4)如图1,过点P作![]() 轴于点E,
轴于点E,
![]() ,
,![]() ,
,![]()
在![]() 中,
中,![]()
即![]()
化简,得![]()
∴y关于x的函数解析式为![]() .
.
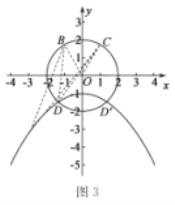
(5)连接![]() ,易得
,易得![]() ,又
,又![]()
∴![]() 为等边三角形,∴
为等边三角形,∴![]()
当![]() 时,在
时,在![]() 的外接圆上,弧
的外接圆上,弧![]() 所对的圆心角为60°
所对的圆心角为60°
其圆心在![]() 的垂直平分线y轴上,
的垂直平分线y轴上,
∴![]() 的外接圆圆心为坐标原点O,
的外接圆圆心为坐标原点O,
设![]() ,则
,则![]() ,即
,即![]() ①
①
又点D在该抛物线上
∴![]() ②
②
由①②联立解得:![]() (舍去)
(舍去)
数形结合可得,
当![]() 时,点D的纵坐标
时,点D的纵坐标![]() 的取值范围为
的取值范围为
![]()

