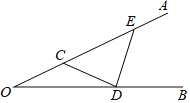
【题目】如图所示,OC=CD=DE,点D,E分别在OB,OA上.若∠BDE=78°,则∠CDE=_____.
【答案】76°
【解析】
根据OC=CD=DE,可得∠O=∠ODC,∠DCE=∠DEC,根据三角形的外角性质可知∠DCE=∠O+∠ODC=2∠ODC,进一步根据三角形的外角性质可知∠BDE=3∠ODC=78°,即可求出∠ODC的度数,进而求出∠CDE的度数.
解:∵OC=CD=DE,
∴∠O=∠ODC,∠DCE=∠DEC,
∴∠DCE=∠O+∠ODC=2∠ODC,
∵∠O+∠OED=3∠ODC=∠BDE=78°,
∴∠ODC=26°,
∵∠CDE+∠ODC=180°﹣∠BDE=102°,
∴∠CDE=102°﹣∠ODC=76°.
故答案为:76°.

