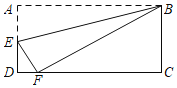
【题目】如图,已知矩形纸片ABCD的两边AB:BC=2:1,过点B折叠纸片,使点A落在边CD上的点F处,折痕为BE.若AB的长为4,则EF的长为( )
A. 8-4![]() B. 2
B. 2![]() C. 4
C. 4![]() 6D.
6D. ![]()
参考答案:
【答案】A
【解析】
由翻折的性质可知:BF=AB=4,AE=EF,设AE=EF=x,在Rt△DEF中,利用勾股定理构建方程即可解决问题.
解:∵AB=4,AB:BC=2:1,
∴BC=2,
∵四边形ABCD是矩形,
∴AD=BC=2,CD=AB=4,∠D=∠C=90°,
由翻折的性质可知:BF=AB=4,AE=EF,设AE=EF=x,
∴CF=![]() ,
,
在Rt△DEF中,
∵DE2+DF2=EF2,
∴(2-x)2+(4-2![]() )2=x2,
)2=x2,
x=8-4![]() .
.
故选A.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形ABCD是正方形,点G是BC边上任意一点,DE⊥AG于点E,BF∥DE且交AG于点F.
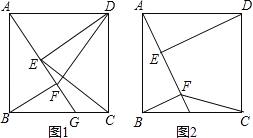
(1)求证:AE=BF;
(2)如图1,连接DF、CE,探究线段DF与CE的关系并证明;
(3)如图2,若AB=
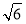 ,G为CB中点,连接CF,直接写出四边形CDEF的面积.
,G为CB中点,连接CF,直接写出四边形CDEF的面积. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在
 中,点
中,点 是
是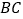 的中点,点
的中点,点 是线段
是线段 的延长线上的一动点,连接
的延长线上的一动点,连接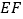 ,过点
,过点 作
作 的平行线
的平行线 ,与线段
,与线段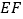 的延长线交于点
的延长线交于点 ,连接
,连接 、
、 .
.
 求证:四边形
求证:四边形 是平行四边形.
是平行四边形. 若
若 ,
, ,则在点
,则在点 的运动过程中:
的运动过程中:①当
 ________时,四边形
________时,四边形 是矩形,试说明理由;
是矩形,试说明理由;②当
 ________时,四边形
________时,四边形 是菱形.
是菱形. -
科目: 来源: 题型:
查看答案和解析>>【题目】根据下面给出的数轴,解答下面的问题:

(1)请你根据图中A,B两点的位置,分别写出它们所表示的有理数A: B: ;
(2)观察数轴,与点A的距离为
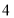 的点表示的数是: ;
的点表示的数是: ;(3)若将数轴折叠,使得
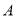 点与0表示的点重合,则B点与数 表示的点重合;
点与0表示的点重合,则B点与数 表示的点重合;(4)若数轴上M、N两点之间的距离为2019(M在N的左侧),且M、N两点经过(3)中折叠后互相重合,则
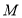 、
、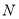 两点表示的数分别是:M: ,N: .
两点表示的数分别是:M: ,N: . -
科目: 来源: 题型:
查看答案和解析>>【题目】数轴上点A对应的数是﹣1,B点对应的数是1,一只小虫甲从点B出发沿着数轴的正方向以每秒4个单位的速度爬行至C点,再立即返回到A点,共用了4秒钟.
(1)求点C对应的数;
(2)若小虫甲返回到A点后再作如下运动:第1次向右爬行2个单位,第2次向左爬行4个单位,第3次向右爬行6个单位,第4次向左爬行8个单位,…依次规律爬下去,求它第10次爬行所停在点所对应的数;
(3)若小虫甲返回到A后继续沿着数轴的负方向以每秒4个单位的速度爬行,这时另一小虫乙从点C出发沿着数轴的负方向以每秒7个单位的速度爬行,设甲小虫对应的点为E点,乙小虫对应的点为F点,设点A、E、F、B所对应的数分别是xA、xE、xF、xB,当运动时间t不超过1秒时,请你结合数轴求出 |xA﹣xE |﹣|xE﹣xF |+ |xF﹣xB |= .(直接写出答案)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,正方形纸片ABCD的边长为2,翻折∠B、∠D,使两个直角的顶点重合于对角线BD上一点P、EF、GH分别是折痕(如图2).设AE=x(0<x<2),给出下列判断:①当x=1时,点P是正方形ABCD的中心;②当x=
 时,EF+GH>AC;③当0<x<2时,六边形AEFCHG面积的最大值是3;④当0<x<2时,六边形AEFCHG周长的值不变.其中正确的选项是( )
时,EF+GH>AC;③当0<x<2时,六边形AEFCHG面积的最大值是3;④当0<x<2时,六边形AEFCHG周长的值不变.其中正确的选项是( )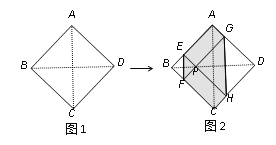
A. ①③ B. ①②④ C. ①③④ D. ①②③④
-
科目: 来源: 题型:
查看答案和解析>>【题目】在求两位数的平方时,可以用“列竖式”的方法进行速算,求解过程如图1所示.仿照图1,用“列竖式”的方法计算一个两位数的平方,部分过程如图2所示,若这个两位数的个位数字为a,则这个两位数为( )
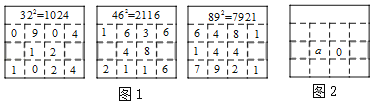
A.a﹣50B.a+50C.a﹣20D.a+20
相关试题

