【题目】如图,直线![]() 和双曲线
和双曲线![]() 相交于点A(1,2)和点B(n,-1).
相交于点A(1,2)和点B(n,-1).
(1)求m,k的值;
(2)不等式![]() 的解集为 ;
的解集为 ;
(3)以A、B、O、P为顶点的平行四边形,顶点P的坐标是 .

参考答案:
【答案】(1)m=1,k=2;
(2)x>1或-2<x<0;
(3)P1(3,3)或P2(-1,1)或P3(-3,-3)
【解析】分析:(1)先把A(1,2)代入直线y=x+m求出m的值,再代入双曲线y=![]() 求出k的值即可;(2)把B(n,-1)一次函数求出n的值,故可得出其坐标,利用函数图象可直接得出不等式的取值范围;(3)设P(x,y),再分OA,AP,AB分别为平行四边形的对角线求出x、y的值即可.
求出k的值即可;(2)把B(n,-1)一次函数求出n的值,故可得出其坐标,利用函数图象可直接得出不等式的取值范围;(3)设P(x,y),再分OA,AP,AB分别为平行四边形的对角线求出x、y的值即可.
本题解析:(1)∵点A(1,2)是直线y=x+m与双曲线y=![]() 的交点,
的交点,
∴1+m=2,解得m=1;k=1×2=2;
(2)∵点B在直线y=x+1上,∴n+1=1,解得n=2,∴n(2,1).
由函数图象可知,当2<x<0或x>1时,一次函数y=x+m的图象在反比例函数y=![]() 图象的上方。
图象的上方。
(3)设P(x,y),∵A(1,2),B(2,1),O(0,0),
∴当OA为平行四边形的对角线时,2+x=1,y1=2,解得x=3,y=3,∴ ![]() (3,3);
(3,3);
当AP为平行四边形的对角线时,x+1=2,y+2=1,解得x=3,y=3,
∴![]() (3,3);
(3,3);
当AB为平行四边形的对角线时,x=12=1,y=21=1,
∴![]() (1,1).
(1,1).
综上所述,P点坐标为![]() (3,3),
(3,3), ![]() (3,3).
(3,3).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AD是BC边上的中线,E是AD的中点,过点A作BC的平行线交BE的延长线于点F,连接CF.
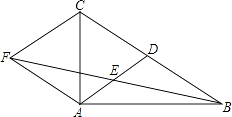
(1)求证:AF=DC;
(2)若AB⊥AC,试判断四边形ADCF的形状,并证明你的结论. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中,点O是边AC上一个动点,过O作直线MN∥BC.设MN交∠ACB的平分线于点E,交∠ACB的外角平分线于点F.

(1)求证:OE=OF;
(2)若CE=8,CF=6,求OC的长;
(3)当点O在边AC上运动到什么位置时,四边形AECF是矩形?并说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】下列这组数据:15、13、14、13、16、13的众数是___________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,把矩形ABCD沿EF翻折,点B恰好落在AD边的B′处,若AE=2,DE=6,∠EFB=60°,则矩形ABCD的面积是( )
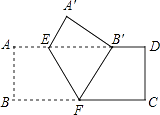
A.12
B.24
C.12
D.16
-
科目: 来源: 题型:
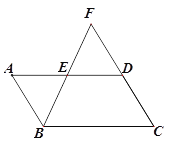
查看答案和解析>>【题目】如图,□ABCD中,E为AD的中点,BE、CD相交于点F.
(1)求证:AB=DF
(2)若△DEF的面积为S1,△BCF的面积为S2,且S12-S2+4=0,求□ABCD的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,矩形ABCD中,AB=3,BC=4,点P从A点出发,按A→B→C的方向在AB和BC上移动.记PA=x,点D到直线PA的距离为y,则y关于x的函数关系的大致图像是( )
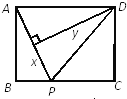
A.
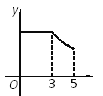 B.
B. 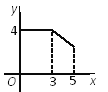 C.
C. 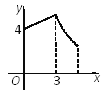 D.
D. 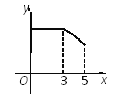
相关试题

