【题目】如图,已知以△ABC的BC边上一点O为圆心的圆,经过A,B两点,且与BC边交于点E,D为弧BE的中点,连接AD交OE于点F,若AC=FC
(Ⅰ)求证:AC是⊙O的切线;
(Ⅱ)若BF=5,DF=![]() ,求⊙O的半径.
,求⊙O的半径.

参考答案:
【答案】(1)证明见解析;(2)4.
【解析】
试题分析:(1)连接OA、OD,求出∠D+∠OFD=90°,推出∠CAF=∠CFA,∠OAD=∠D,求出∠OAD+∠CAF=90°,根据切线的判定推出即可;
(2)OD=r,OF=8﹣r,在Rt△DOF中根据勾股定理得出方程r2+(8﹣r)2=(![]() )2,求出即可.
)2,求出即可.
试题解析:(1)连接OA、OD,

∵D为弧BE的中点,
∴OD⊥BC,
∠DOF=90°,
∴∠D+∠OFD=90°,
∵AC=FC,OA=OD,
∴∠CAF=∠CFA,∠OAD=∠D,
∵∠CFA=∠OFD,
∴∠OAD+∠CAF=90°,
∴OA⊥AC,
∵OA为半径,
∴AC是⊙O切线;
(2)∵⊙O半径是r,
∴OD=r,OF=5﹣r,
在Rt△DOF中,r2+(5﹣r)2=(![]() )2,
)2,
r=4,r=1(舍),
即⊙O的半径r为4.
-
科目: 来源: 题型:
查看答案和解析>>【题目】若一正n边形的一个外角不大于40°,则这个多边形可能是______.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在下列条件中:①∠A+∠B=∠C,②∠A:∠B:∠C=1: 2:3,③∠A=90°﹣∠B,④∠A=∠B=∠C中,能确定△ABC是直角三角形的条件有( )
A. 1个 B. 2个 C. 3个 D. 4个
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知二次函数y=ax2+bx+8(a≠0)的图象与x轴交于点A(﹣2,0),
B(4,0)与y轴交于点C.
(Ⅰ)求抛物线的解析式及其顶点D的坐标;
(Ⅱ)求△BCD的面积;
(Ⅲ)若直线CD交x轴与点E,过点B作x轴的垂线,交直线CD与点F,将抛物线沿其对称轴向上平移,使抛物线与线段EF总有公共点.试探究抛物线最多可以向上平移多少个单位长度(直接写出结果,不写求解过程).

-
科目: 来源: 题型:
查看答案和解析>>【题目】我们知道,无限循环小数都可以转化为分数.例如:将
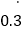 转化为分数时,可设
转化为分数时,可设 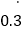 =x,则x=0.3+
=x,则x=0.3+ 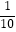 x,解得x=
x,解得x=  ,即
,即 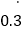 =
=  .仿此方法,将
.仿此方法,将 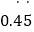 化成分数是 .
化成分数是 . -
科目: 来源: 题型:
查看答案和解析>>【题目】当x+y=3时,5﹣x﹣y等于( )
A. 6 B. 4 C. 2 D. 3
-
科目: 来源: 题型:
查看答案和解析>>【题目】去年某省将地处A、B两地的两所大学合并成一所综合大学,为了方便A、B两地师生的交往,学校准备在相距5km的A、B两地之间修筑一条笔直的公路,已知在C地有一个以C为圆心,半径为2km的果园,而且AC=4km,BC=3km,问:计划修筑的这条公路会不会穿过该果园?为什么?
相关试题

