搜索
【题目】把下列各数填在相应的横线上．
，－
，
，0.5，2π，3.14159265，－|－
|，1.3030030003…(每相邻两个3之间依次多一个0)．
(1)有理数：______________________________________________________；
(2)无理数：_________________________________________________________；
(3)正实数：__________________________________________________________；
(4)负实数：__________________________________________________________.
参考答案：
【答案】 －
，
，0.5，3.14159265，－|－
| 
，2π，1.3030030003…(每相邻两个3之间依次多一个0) ，0.5，2π，3.14159265，1.3030030003…(每相邻两个3之间依次多一个0) －，，－|－|
【解析】根据实数的分类分别进行填写即可.
（1）有理数：－，
，0.5，3.14159265，－|－|；
（2）无理数：，2π，1.3030030003…(每相邻两个3之间依次多一个0)；
（3）正实数：，0.5，2π，3.14159265，1.3030030003…(每相邻两个3之间依次多一个0)；
（4）负实数：－，，－|－|
-
科目： 来源： 题型：
查看答案和解析>>【题目】某市水果批发部门欲将A市的一批水果运往本市销售，有火车和汽车两种运输方式，运输过程中的损耗均为200元/时，其他主要参考数据如下：
运输工具
途中平均速度
(千米/时)
运费
(元/千米)
装卸费用
(元)
火车
100
15
2000
汽车
80
20
900
(1)如果选择汽车的总费用比选择火车的总费用多1100元，那么你知道本市与A市之间的路程是多少千米吗？请你列方程解答；
(2)若A市与某市之间的路程为s千米，且知道火车与汽车在路上耽误的时间分别为2小时和3.1小时，要想将这批水果运往该市进行销售，则当s为多少时，选择火车和汽车运输所需费用相同？
-
科目： 来源： 题型：
查看答案和解析>>【题目】分解因式2a（b+c）-3（b+c）的结果是______.
【答案】（b+c）（2a-3）
【解析】解析：2a（b+c）-3（b+c）=（b+c）（2a-3）.
点睛：因式分解的方法：（1）提取公因式法.ma+mb+mc=m(a+b+c).
（2）公式法:完全平方公式，平方差公式.
（3）十字相乘法.
因式分解的时候，要注意整体换元法的灵活应用，训练将一个式子看做一个整体,利用上述方法因式分解的能力.
【题型】填空题
【结束】
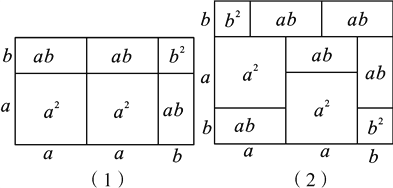
17【题目】在我们所学的课本中，多项式与多项式相乘可以用几何图形的面积来表示.例如，（2a+b）（a+b）=2a2+3ab+b2就可以用图（1）来表示.请你根据此方法写出图（2）中图形的面积所表示的代数恒等式：____________.
-
科目： 来源： 题型：
查看答案和解析>>【题目】阅读下面的解题过程：
计算：(－15)÷
×6.解：原式＝(－15)÷
×6(第一步)＝(－15)÷(－1)(第二步)
＝－15.(第三步)
回答：(1)上面解题过程中有两处错误，第一处是第________步，错误的原因是________________；第二处是第________，错误的原因是________________．
(2)把正确的解题过程写出来．
-
科目： 来源： 题型：
查看答案和解析>>【题目】在我们所学的课本中，多项式与多项式相乘可以用几何图形的面积来表示.例如，（2a+b）（a+b）=2a2+3ab+b2就可以用图（1）来表示.请你根据此方法写出图（2）中图形的面积所表示的代数恒等式：____________.
【答案】（a+2b）（2a+b）=2a2+5ab+2b2
【解析】试题分析：图②的面积可以用长为a+a+b，宽为b+a+b的长方形面积求出，也可以由四个正方形与5个小长方形的面积之和求出，表示出即可．
解：根据图形列得：（a+2b）（2a+b）=2a2+5ab+2b2．
故答案为：（a+2b）（2a+b）=2a2+5ab+2b2．
考点：多项式乘多项式．
点评：此题考查了多项式乘以多项式法则，熟练掌握法则是解本题的关键．
【题型】填空题
【结束】
18【题目】若一个正整数能表示为两个正整数的平方差，则称这个正整数为“智慧数”（如3=22-12，16=52-32，则3和16是智慧数）.已知按从小到大的顺序构成如下数列：3，5，7，8，9，11，12，13，15，16，17，19，20，21，23，24，25，…则第2 013个“智慧数”是______.
-
科目： 来源： 题型：
查看答案和解析>>【题目】若一个正整数能表示为两个正整数的平方差，则称这个正整数为“智慧数”（如3=22-12，16=52-32，则3和16是智慧数）.已知按从小到大的顺序构成如下数列：3，5，7，8，9，11，12，13，15，16，17，19，20，21，23，24，25，…则第2 013个“智慧数”是______.
【答案】2 687
【解析】解析：观察数的变化规律，可知全部“智慧数”从小到大可按每三个数分一组，从第2组开始每组的第一个数都是4的倍数，归纳可得，第n组的第一个数为4n（n≥2）.因为2 013÷3=671，所以第2 013个“智慧数”是第671组中的第3个数，即为4×671+3=2 687.
点睛：找规律题需要记忆常见数列
1,2,3,4……n
1,3,5,7……2n-1
2,4,6,8……2n
2,4,8,16,32……
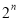
1,4,9,16,25……
2,6,12,20……n(n+1)
一般题目中的数列是利用常见数列变形而来，其中后一项比前一项多一个常数，是等差数列，列举找规律.后一项是前一项的固定倍数，则是等比数列，列举找规律.
【题型】填空题
【结束】
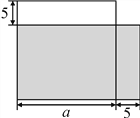
19【题目】如图，郑某把一块边长为a m的正方形的土地租给李某种植，他对李某说：“我把你这块地的一边减少5 m，另一边增加5 m，继续租给你，你也没有吃亏，你看如何”.李某一听，觉得自己好像没有吃亏，就答应了.同学们，你们觉得李某有没有吃亏？请说明理由.
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，平行四边形ABCD的周长是26cm，对角线AC与BD交于点O，AC⊥AB，E是BC中点，△AOD的周长比△AOB的周长多3cm，则AE的长度为（ ）
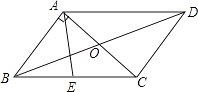
A.3cm
B.4cm
C.5cm
D.8cm
相关试题
