搜索
【题目】在数1，0，﹣1，﹣2中，最大的数是（ ）
A.1
B.0
C.﹣1
D.﹣2
参考答案：
【答案】A
【解析】解：由正数大于零，零大于负数，得
1＞0＞﹣1＞﹣2，
故选：A．
根据正数大于零，零大于负数，可得答案．
-
科目： 来源： 题型：
查看答案和解析>>【题目】已知a是2的相反数，计算|a一2|的值．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，将等边△ABC绕点C顺时针旋转120°得到△EDC，连接AD，BD．则下列结论：
①AC=AD；②BD⊥AC；③四边形ACED是菱形．
其中正确的个数是（ ）
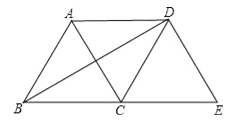
A．0 B．1 C．2 D．3
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图1在正方形ABCD的外侧作两个等边三角形ADE和DCF，连接AF，BE．
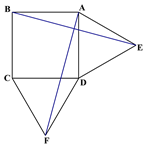
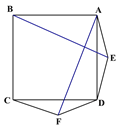
（图1） （图2） （备用图）
（1）请判断：AF与BE的数量关系是_____________，位置关系______________；
（2）如图2，若将条件“两个等边三角形ADE和DCF”变为“两个等腰三角形ADE和DCF，且EA=ED=FD=FC”，第（1）问中的结论是否仍然成立？请作出判断并给予证明；
（3）若三角形ADE和DCF为一般三角形，且AE=DF，ED=FC，第（1）问中的结论都能成立吗？请直接写出你的判断．
-
科目： 来源： 题型：
查看答案和解析>>【题目】据科学家估计，地球年龄大约是4 600 000 000年，这个数用科学记数法表示为（ ）
A.4.6×108
B.46×108
C.4.6×109
D.0.46×1010 -
科目： 来源： 题型：
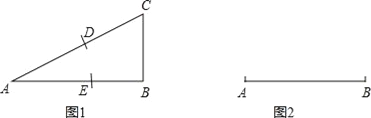
查看答案和解析>>【题目】（1）如图1，Rt△ABC中，∠B=90°，AB=2BC，现以C为圆心、CB长为半径画弧交边AC于D，再以A为圆心、AD为半径画弧交边AB于E．求证：
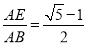．（这个比值
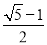叫做AE与AB的黄金比．）（2）如果一等腰三角形的底边与腰的比等于黄金比，那么这个等腰三角形就叫做黄金三角形．请你以图2中的线段AB为腰，用直尺和圆规，作一个黄金三角形ABC．
（注：直尺没有刻度！作图不要求写作法，但要求保留作图痕迹，并对作图中涉及到的点用字母进行标注）
-
科目： 来源： 题型：
查看答案和解析>>【题目】数学问题：计算
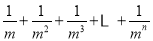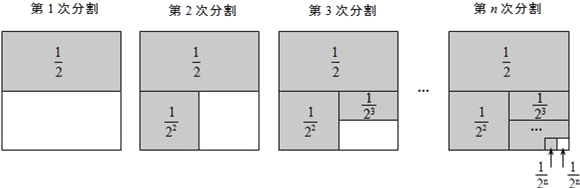
（其中m，n都是正整数，且m≥2，n≥1）．探究问题：为解决上面的数学问题，我们运用数形结合的思想方法，通过不断地分割一个面积为1的正方形，把数量关系和几何图形巧妙地结合起来，并采取一般问题特殊化的策略来进行探究．
探究一：计算
．第1次分割，把正方形的面积二等分，其中阴影部分的面积为
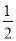；第2次分割，把上次分割图中空白部分的面积继续二等分，阴影部分的面积之和为
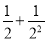；第3次分割，把上次分割图中空白部分的面积继续二等分，…；
…
第n次分割，把上次分割图中空白部分的面积最后二等分，所有阴影部分的面积之和为
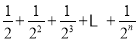，最后空白部分的面积是
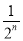．根据第n次分割图可得等式：
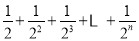=1﹣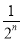
．
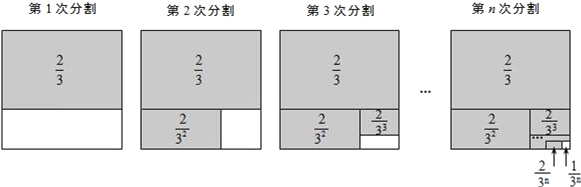
探究二：计算
．第1次分割，把正方形的面积三等分，其中阴影部分的面积为
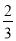；第2次分割，把上次分割图中空白部分的面积继续三等分，阴影部分的面积之和为
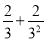；第3次分割，把上次分割图中空白部分的面积继续三等分，…；
…
第n次分割，把上次分割图中空白部分的面积最后三等分，所有阴影部分的面积之和为
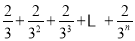，最后空白部分的面积是
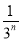．根据第n次分割图可得等式：
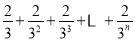=1﹣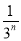
，两边同除以2，得
=
.
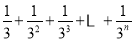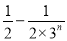探究三：计算
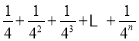．（仿照上述方法，只画出第n次分割图，在图上标注阴影部分面积，并写出探究过程）
解决问题：计算
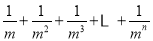．（只需画出第n次分割图，在图上标注阴影部分面积，并完成以下填空）
根据第n次分割图可得等式： ，
所以，
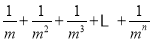= ．拓广应用：计算
．
相关试题
