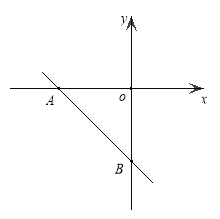
【题目】如图,在平面直角坐标系中,一次函数![]() 分别与x轴、y轴相交于A、B两点,二次函数
分别与x轴、y轴相交于A、B两点,二次函数![]() 的图像经过点A.
的图像经过点A.
(1)试证明二次函数![]() 的图像与x轴有两个交点;
的图像与x轴有两个交点;
(2)若二次函数![]() 图像的顶点D在直线AB上,求m,n的值;
图像的顶点D在直线AB上,求m,n的值;
(3)设二次函数![]() 的图像与x轴的另一个交点为点C,顶点D关于x轴的对称点设为点E,以AE,AC为邻边作平行四边形EACF,顶点F能否在该二次函数的图像上?如果在,求出这个二次函数的表达式;如果不在,请说明理由?
的图像与x轴的另一个交点为点C,顶点D关于x轴的对称点设为点E,以AE,AC为邻边作平行四边形EACF,顶点F能否在该二次函数的图像上?如果在,求出这个二次函数的表达式;如果不在,请说明理由?
参考答案:
【答案】(1)证明见解析(2)4,3;6,9(3)P(-1,![]() )
)
【解析】
试题分析:(1)根据待定系数法求得二次函数的解析式,然后根据根的判别式可证明;
(2)根据二次函数的顶点坐标可求的m,n的值;
(3)根据B点的坐标求得m的值,即可得二次函数的解析式,然后设E点的横坐标为t,求得E点的坐标,再求得直线AE,由此求得P点的坐标.
试题解析:(1)A(﹣3,0),B(0,﹣3),
二次函数![]() 的图像经过点C(-6,18-n),则n=3m﹣9,
的图像经过点C(-6,18-n),则n=3m﹣9,
即![]() .
.
∵![]() =
=![]() =
=![]() ,
,
又![]() ,
,
∴![]() ,
,
则二次函数![]() 的图像与x轴有两个交点;
的图像与x轴有两个交点;
(2)二次函数![]() ,即
,即![]()
顶点坐标为(![]() ,
,![]() ),
),
因为二次函数![]() 图像的顶点在直线AB上,
图像的顶点在直线AB上,
所以![]() ,解得:
,解得:![]() ,
,![]() ,
,
则![]() ,
,![]() ;
;
(3)抛物线![]() 过点B(0,-3),
过点B(0,-3),
则m=2
此时函数关系式为![]() ,易证点A在抛物线上.
,易证点A在抛物线上.
设点E的横坐标为t,则(-3+1)(t +1)=![]()
∴![]() , 求得点E的坐标为(
, 求得点E的坐标为(![]() ,
,![]() ),
),
则直线AE对应的函数关系式:![]() ,
,
求得点P(-1,![]() ).
).
-
科目: 来源: 题型:
查看答案和解析>>【题目】河水的平均深度为2.5米,一个身高1.5米但不会游泳的人下水后( )
A.肯定会淹死B.不一定会淹死C.淹不死D.以上答案都不对
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,E、F分别是□ABCD的边BC、AD上的中点.

(1) 求证:△ABE≌△CDF;
(2) 当∠BAC= ° 时,四边形AECF是菱形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠C=90°,AB的垂直平分线DE交AC于D,垂足为E,若∠A=30°,CD=3.
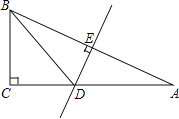
(1)求∠BDC的度数.
(2)求AC的长度.
-
科目: 来源: 题型:
查看答案和解析>>【题目】垃圾的分类处理与回收利用,可以减少污染,节省资源,生活垃圾一般按如图所示A、B、C、D四种分类方法回收处理,某城市环保部门为了提高宣传实效,抽样调查、统计了部分居民小区一段时间内生活垃圾的分类处理情况,并将调查统计结果绘制成如下两幅不完整的统计图表:
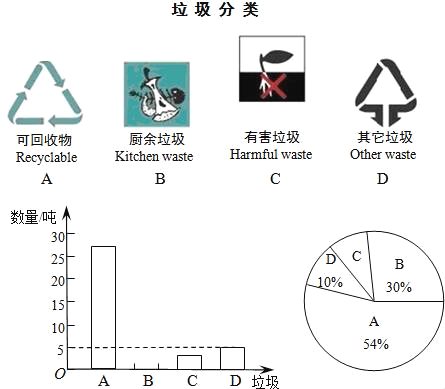
根据图表解答下列问题:
(1)请将条形统计图补充完整;
(2)在抽样数据中,产生的有害垃圾共 吨;
(3)调查发现,在可回收物中塑料类垃圾占
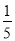 ,每回收1吨塑料类垃圾可获得0.7吨二级原料.假设该城市每月产生的生活垃圾为5000吨,且全部分类处理,那么每月回收的塑料类垃圾可以获得多少吨二级原料?
,每回收1吨塑料类垃圾可获得0.7吨二级原料.假设该城市每月产生的生活垃圾为5000吨,且全部分类处理,那么每月回收的塑料类垃圾可以获得多少吨二级原料? -
科目: 来源: 题型:
查看答案和解析>>【题目】三名大学生竞选系学生会主席,他们的笔试成绩和口试成绩(单位:分)分别用了两种方式进行了统计,如表一和图一:
(1)请将表一和图一中的空缺部分补充完整.
(2)竞选的最后一个程序是由本系的300名学生进行投票,三位候选人的得票情况如图二(没有弃权票,每名学生只能推荐一个),请计算每人的得票数.
(3)若每票计1分,系里将笔试、口试、得票三项测试得分按
 的比例确定个人成绩,请计算三位候选人的最后成绩,并根据成绩判断谁能当选.
的比例确定个人成绩,请计算三位候选人的最后成绩,并根据成绩判断谁能当选.
-
科目: 来源: 题型:
查看答案和解析>>【题目】国家对电信资费进行了调整,区内(主城区或县内)的收费标准是月租费25元,首次3分钟0.2元(不足3分钟按3分钟计),以后每分钟0.1元(不足1分钟计为1分钟),若本月该用户区内电话累计通话100分钟,共通话30次,问他本月至少要缴纳区内话费_____元;
相关试题

