【题目】用配方法解方程:x2﹣2x﹣4=0
参考答案:
【答案】解:把方程x2﹣2x﹣4=0的常数项移到等号的右边,得到x2﹣2x=4,
方程两边同时加上一次项系数一半的平方,得到x2﹣2x+1=4+1,
配方得(x﹣1)2=5,
∴x﹣1=±![]() ,
,
∴x1=1﹣![]() ,x2=1+
,x2=1+![]() .
.
【解析】按照配方法的一般步骤计算:(1)把常数项移到等号的右边;(2)把二次项的系数化为1;(3)等式两边同时加上一次项系数一半的平方.选择用配方法解一元二次方程时,最好使方程的二次项的系数为1,一次项的系数是2的倍数.
【考点精析】根据题目的已知条件,利用配方法的相关知识可以得到问题的答案,需要掌握左未右已先分离,二系化“1”是其次.一系折半再平方,两边同加没问题.左边分解右合并,直接开方去解题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知x+12的算术平方根是
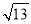 ,2x+y﹣6的立方根是2.
,2x+y﹣6的立方根是2. (1)求x,y的值;
(2)求3xy的平方根.
-
科目: 来源: 题型:
查看答案和解析>>【题目】为推进“传统文化进校园”活动,某校准备成立“经典诵读”、“传统礼仪”、“民族器乐”和“地方戏曲”等四个课外活动小组.学生报名情况如图(每人只能选择一个小组):

(1)报名参加课外活动小组的学生共有 人,将条形图补充完整;
(2)扇形图中m= ,n= ;
(3)根据报名情况,学校决定从报名“经典诵读”小组的甲、乙、丙、丁四人中随机安排两人到“地方戏曲”小组,甲、乙恰好都被安排到“地方戏曲”小组的概率是多少?请用列表或画树状图的方法说明.
-
科目: 来源: 题型:
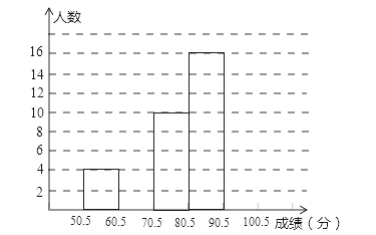
查看答案和解析>>【题目】为了让学生了解环保知识,增强环保意识,某中学举行了一次“环保知识竞赛”,共有850名学生参加了这次竞赛,为了解本次竞赛成绩情况,从中抽取了部分学生的成绩(得分取整数,满分为100分)进行统计.请你根据尚未完成并有局部污染的频率分布表和频率分布直方图,解答下列问题:
分 组
频数
频率
50.5~60.5
4
0.08
60.5~70.5
0.16
70.5~80.5
10
80.5~90.5
16
0.32
90.5~100.5
合 计
50
1.00
(1)填充频率分布表的空格;
(2)补全频数直方图,并在此图上直接绘制频数分布折线图;
(3)全体参赛学生中,竞赛成绩落在哪组范围内的人数最多?
(4)若成绩在90分以上(不含90分)为优秀,则该校成绩优秀的约为多少人?
-
科目: 来源: 题型:
查看答案和解析>>【题目】二次函数y=x2﹣2x+1的图象与坐标轴的交点个数是( )
A.0B.1C.2D.3
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知|x|=4,|y|=5,且xy<0,则x+y的值等于( )
A. 9或﹣9B. 9或﹣1C. 1或﹣1D. ﹣9或﹣1
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列各组数中,结果一定相等的为( )
A. ﹣a2与(﹣a)2B. ﹣(﹣a)2与a2
C. ﹣a2与﹣(﹣a)2D. (﹣a)2与﹣(﹣a)2
相关试题

