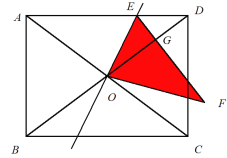
【题目】如图，矩形ABCD中，AB＝3，BC＝4，对角线AC，BD相交于点O，点E是AD边上一动点，将△AEO沿直线EO折叠，点A落在点F处，线段EF，OD相交于点G．若△DEG是直角三角形，则线段DE的长为____________

【答案】或．

【解析】

分情况讨论：当∠EGD＝90°时，设DE＝x，先利用勾股定理求得AC＝BD＝5，进而可求得tan∠ADB＝，sin∠GFO＝，cos∠ADB＝，进而表示出DG＝x，OG＝OD－DG＝－x，最后根据sin∠GFO＝列出方程求解即可；当∠GED＝90°时，则由折叠知，∠AEO＝∠OEF＝45°，过点O作OH⊥AD于H，设DE＝x，则EH＝HD－DE＝2－x，再根据tan∠ADO＝列出方程求解即可．

（1）当∠EGD＝90°时，如图，设DE＝x，

∵在矩形ABCD中，AB＝3，BC＝4，∠ABC＝∠BAD＝∠ADC＝90°，

∴AC＝BD＝，AD＝BC＝4，CD＝AB＝3，

∴OA＝OD＝BD＝，

∵将△AEO沿直线EO折叠，点A落在点F处，

∴OF＝OA＝，∠DAC＝∠F，

∴在Rt△ABD中，tan∠ADB＝，

同理可得：sin∠GFO＝，cos∠ADB＝，

∵在Rt△DEG中，cos∠EDG＝

∴DG＝x，

∴OG＝OD－DG＝－x，

∵在Rt△OGF中，sin∠GFO＝

∴，

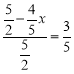解得：x＝；

（2）当∠GED＝90°时，

则由折叠知，∠AEO＝∠OEF＝45°，

过点O作OH⊥AD于H，如图所示，

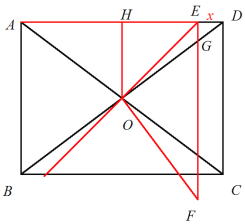
∴△EHO为等腰直角三角形，HE＝HO，

∵OA＝OD，OH⊥AD，

∴HD＝AD＝2，

设DE＝x，则EH＝HD－DE＝2－x，

∴OH＝EH＝2－x，

∵tan∠ADO＝，

∴，

解得：x＝；

∴综上所述，DE的长为或．

故答案为：或．

关闭