【题目】如图,互相垂直的两条射线OE与OF的端点O在三角板的内部,与三角板两条直角边的交点分别为点D、B.
(1)填空:若∠ABO=50°,则∠ADO= ;
(2)若DC、BP分别是∠ADO、∠ABF的角平分线,如图1.求证:DC⊥BP;
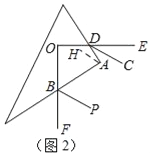
(3)若DC、BP分别分别是∠ADE、∠ABF的角平分线,如图2.猜想DC与BP的位置关系,并说明理由.
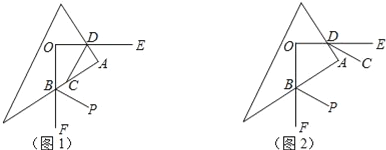
参考答案:
【答案】(1)130°;(2)证明见解析,(3)DC与BP互相平行.理由见解析.
【解析】试题分析:(1)由四边形的内角和为360°即可得;
(2)如图1,延长DC交BP于G,由∠OBA+∠ODA=180°、∠OBA+∠ABF=180°可得∠ODA=∠ABF,再由DC、BP分别是∠ADO、∠ABF的角平分线,从而可得∠CDA=∠CBG,再由∠DCA=∠BCG,继而可得∠BGC=∠A=90°,即得DC⊥BP;
(3)DC与BP互相平行.如图2,作过点A作AH∥BP,则可得∠ABP=∠BAH,由∠OBA+∠ODA=180°,可得∠ABF+∠ADE=180°,再由DC、BP分别分别是∠ADE、∠ABF的角平分线,从而可得∠ADC+∠ABP=90°,进而可得∠DAH=∠ADC,从而可得CD∥AH,最后得CD∥BP.
试题解析:(1)如图1,∵OE⊥OF,∴∠EOF=90°,
在四边形OBAD中,∠A=∠BOD=90°,∠ABO=50°,
∴∠ADO=360°﹣90°﹣90°﹣50°=130°;
故答案为:130°;
(2)如图1,延长DC交BP于G,
∵∠OBA+∠ODA=180°,而∠OBA+∠ABF=180°,∴∠ODA=∠ABF,
∵DC、BP分别是∠ADO、∠ABF的角平分线,∴∠CDA=∠CBG,
而∠DCA=∠BCG,∴∠BGC=∠A=90°,∴DC⊥BP;

(3)DC与BP互相平行.
理由:如图2,作过点A作AH∥BP,则∠ABP=∠BAH,
∵∠OBA+∠ODA=180°,∴∠ABF+∠ADE=180°,
∵DC、BP分别分别是∠ADE、∠ABF的角平分线,∴∠ADC+∠ABP=90°,
∴∠ADC+∠BAH=90°,
而∠DAH+∠BAH=90°,∴∠DAH=∠ADC,∴CD∥AH,∴CD∥BP.
-
科目: 来源: 题型:
查看答案和解析>>【题目】若一个有理数的平方是正数,则这个有理数的立方是( )
A.正数 B.负数 C.正数或负数 D.整数
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算a3÷a2的结果是( )
A.a5
B.a-1
C.a
D.a2 -
科目: 来源: 题型:
查看答案和解析>>【题目】测得某乒乓球厂生产的五个乒乓球的质量误差(g)如下表.检验时,通常把比标准质量大的克数记为正,比标准质量小的克数记为负.请你选出最接近标准质量的球,是 号.
号码
1
2
3
4
5
误差(g)
0.1
0.2
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知⊙O的直径为10,若PO=5,则点P与⊙O的位置关系是( )
A. 点P在⊙O内 B. 点P在⊙O上 C. 点P在⊙O外 D. 无法判断
-
科目: 来源: 题型:
查看答案和解析>>【题目】解答题
(1)已知am=5,an=4, 求a3m-2n的值.
(2)已知3a-2b=2,求27a÷9b的值.
(3)已知2x÷16y =8,求2x-8y的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】下列各式的运算等于a6的是( )
A.a2a3
B.a12÷a2
C.a3+a3
D.(a3)2
相关试题

