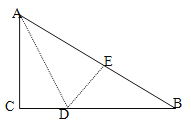
【题目】如图，在Rt△ABC中，∠C=90°，△ACD沿AD折叠，使得点C落在斜边AB上的点E处．
（1）求证：△BDE∽△BAC；
（2）已知AC=6，BC=8，求线段AD的长度．
【答案】(1)、证明过程见解析；(2)、AD=3
【解析】
试题分析：(1)、根据折叠得出∠C=∠BED=90°，结合∠B为公共角得出三角形相似；(2)、首先求出AB的长度，然后设CD=x，根据折叠得出DE和BE的长度，从而根据Rt△BDE的勾股定理求出DE的长度，然后根据Rt△ADE的勾股定理求出AD的长度.
试题解析：(1)、∵∠C=90° 根据折叠图形的性质 ∴∠BED=90° ∴∠C=∠BED 又∵∠B=∠B
∴△BDE∽△BAC
(2)、根据Rt△ABC的勾股定理可得AB=10，设CD=x，则BD=8－x，DE=x，AE=AC=6，则BE=10，
根据Rt△BDE的勾股定理可得：DE=3， 根据Rt△ADE的勾股定理可得：AD=3
阅读快车系列答案科目：初中数学 来源： 题型：
【题目】如图，抛物线y=ax2+bx+2交x轴于A（﹣1，0），B（4，0）两点，交y轴于点C，与过点C且平行于x轴的直线交于另一点D，点P是抛物线上一动点．
（1）求抛物线解析式及点D坐标；
（2）点E在x轴上，若以A，E，D，P为顶点的四边形是平行四边形，求此时点P的坐标；
（3）过点P作直线CD的垂线，垂足为Q，若将△CPQ沿CP翻折，点Q的对应点为Q′．是否存在点P，使Q′恰好落在x轴上？若存在，求出此时点P的坐标；若不存在，说明理由．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，有下列判定，其中正确的有（ ） ①若∠1=∠3，则AD∥BC；
②若AD∥BC，则∠1=∠2=∠3；
③若∠1=∠3，AD∥BC，则∠1=∠2；
④若∠C+∠3+∠4=180°，则AD∥BC．
A.1个
B.2个
C.3个
D.4个
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，Rt△OAB如图所示放置在平面直角坐标系中，直角边OA与x轴重合，∠OAB=90°，OA=4，AB=2，把Rt△OAB绕点O逆时针旋转90°，点B旋转到点C的位置，一条抛物线正好经过点O，C，A三点．
（1）求该抛物线的解析式；
（2）在x轴上方的抛物线上有一动点P，过点P作x轴的平行线交抛物线于点M，分别过点P，点M作x轴的垂线，交x轴于E，F两点，问：四边形PEFM的周长是否有最大值？如果有，请求出最值，并写出解答过程；如果没有，请说明理由．
（3）如果x轴上有一动点H，在抛物线上是否存在点N，使O（原点）、C、H、N四点构成以OC为一边的平行四边形？若存在，求出N点的坐标；若不存在，请说明理由．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com