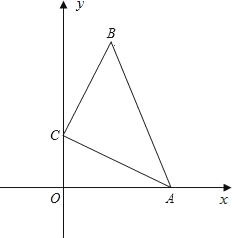
【题目】如图,在直角坐标系中,△ABC满足∠BCA=90°,AC=BC=![]() ,点A、C分别在x轴和y轴上,当点A从原点开始沿x轴的正方向运动时,则点C始终在y轴上运动,点B始终在第一象限运动.
,点A、C分别在x轴和y轴上,当点A从原点开始沿x轴的正方向运动时,则点C始终在y轴上运动,点B始终在第一象限运动.
(1)当AB∥y轴时,求B点坐标.
(2)随着A、C的运动,当点B落在直线y=3x上时,求此时A点的坐标.
(3)在(2)的条件下,在y轴上是否存在点D,使以O、A、B、D为顶点的四边形面积是4?如果存在,请直接写出点D的坐标;如果不存在,请说明理由.
参考答案:
【答案】(1)点B坐标为(![]() ,
,![]() )(2)点A(2,0);(3)存在点D,点D坐标为(0,﹣1)或(0,2).
)(2)点A(2,0);(3)存在点D,点D坐标为(0,﹣1)或(0,2).
【解析】
(1)根据勾股定理,可得AB的长,根据勾股定理,可得AO的长,可得B点坐标;
(2)根据全等三角形的判定与性质,可得BE=OC=x,EC=OA=x,根据勾股定理,可得x的长,可得A点坐标;
(3)分类讨论:①D在y轴的正半轴上;②D在y轴的负半轴上,根据面积的和差,可得关于y的方程,根据解方程,可得答案.
(1)∵∠BCA=90°,AC=BC=![]() ,
,
∴∠BAC=45°,AB=![]() =
=![]()
∵AB∥y轴,
∴∠BAO=90°=∠COA
∴∠CAO=45°=∠OCA
∴CO=AO
∵AO2+CO2=AC2,
∴2AO2=5
∴AO=![]()
∴点B坐标为(![]() ,
,![]() )
)
(2)如图,过点B,作BE⊥y轴,垂足为点E,
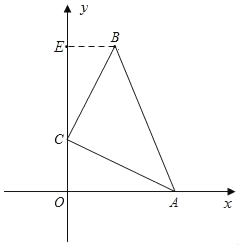
∵∠BCE+∠ACO=90°,∠ACO+∠CAO=90°
∴∠BCE=∠CAO,且AC=BC,∠BEO=∠AOC
∴△AOC≌△CEB(AAS)
∴BE=CO,AO=CE
∵点B落在直线y=3x上
∴设B(x,3x)
∴BE=x=OC,OE=3x,
∴CE=OA=2x,
∵OA2+OC2=AC2
∴(2x)2+x2=5
∴x=1
∴OA=2x=2
∴点A(2,0)
(3)设点D(0,y)
当点D在y轴正半轴上,如图,连接OB,
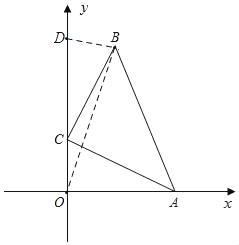
∵S四边形ABDO=S△AOB+S△BDO=4
∴![]() ×y×1+
×y×1+![]() ×2×3=4
×2×3=4
∴y=2
∴点D(0,2)
若点D在y轴负半轴上,如图,连接OB,

∵S四边形ABDO=S△AOB+S△ADO=4
∴![]() ×2×3+
×2×3+![]() ×2×(﹣y)=4
×2×(﹣y)=4
∴y=﹣1
∴点D坐标为(0,﹣1).
∴存在点D,点D坐标为(0,2)或(0,﹣1).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,为了测量某电线杆(底部可到达)的高度,准备了如下的测量工具:
①平面镜;②皮尺;③长为2米的标杆;④高为1.5m的测角仪(测量仰角、俯角的仪器),请根据你所设计的测量方案,回答下列问题:
(1)画出你的测量方案示意图,并根据你的测量方案写出你所选用的测量工具;
(2)结合你的示意图,写出求电线杆高度的思路. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知y是x的一次函数,且当x=0时,y=﹣4;且图象通过点(1,﹣2)
(1)求这个一次函数的解析式;
(2)判断点(a,2a﹣4)是否在该函数图象上,并说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】“母亲节”前夕,我市某校学生积极参与“关爱贫困母亲”的活动,他们购进了一批单价为20元的“孝文化衫”在课余时间进行义卖,并将所得利润捐给贫困母亲.在义卖的过程中发现“这种文化衫每天的销售件数y(件)与销售单价x(元)满足一次函数关系:y=﹣3x+108(20<x<36)”.如果义卖这种文化衫每天的利润为p(元),那么销售单价定为多少元时,每天获得的利润最大?最大利润是多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】某县为了落实中央的“强基惠民工程”,计划将某村的居民自来水管道进行改造.该工程若由甲队单独施工恰好在规定时间内完成;若乙队单独施工,则完成工程所需天数是规定天数的1.5倍.如果由甲、乙队先合做15天,那么余下的工程由甲队单独完成还需5天.
(1)这项工程的规定时间是多少天?
(2)已知甲队每天的施工费用为6500元,乙队每天的施工费用为3500元.为了缩短工期以减少对居民用水的影响,工程指挥部最终决定该工程由甲、乙队合做来完成.则该工程施工费用是多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1所示,从边长为a的正方形纸片中减去一个边长为b的小正方形,再沿着线段AB剪开,把剪成的两张纸拼成如图2的等腰梯形(其面积=
 ).
).(1)设图1中阴影部分面积为S1,图2中阴影部分面积为S2,请直接用含a、b的式子表示S1和S2;
(2)请写出上述过程所揭示的乘法公式.

-
科目: 来源: 题型:
查看答案和解析>>【题目】问题背景:在△ABC中,AB、BC、AC三边的长分别为
 、
、 、
、 ,求此三角形的面积.小辉同学在解答这道题时,先建立一个正方形网格(每个小正方形的边长为1),再在网格中画出格点△ABC(即△ABC三个顶点都在小正方形的顶点处),如图①所示.这样不需求△ABC的高,而借用网格就能计算出它的面积.
,求此三角形的面积.小辉同学在解答这道题时,先建立一个正方形网格(每个小正方形的边长为1),再在网格中画出格点△ABC(即△ABC三个顶点都在小正方形的顶点处),如图①所示.这样不需求△ABC的高,而借用网格就能计算出它的面积.(1)请你将△ABC的面积直接填写在横线上: .
思维拓展:
(2)我们把上述求△ABC面积的方法叫做构图法.如果△ABC三边的长分别
 a、
a、 a、
a、 a(a>0),请利用图②的正方形网格(每个小正方形的边长为a)画出相应的△ABC,并求出它的面积.
a(a>0),请利用图②的正方形网格(每个小正方形的边长为a)画出相应的△ABC,并求出它的面积.
相关试题

