【题目】圆内接四边形ABCD中,∠A:∠B:∠C=2:3:7,则∠D=_____°.
参考答案:
【答案】120
【解析】
根据圆内接四边形对角互补,求出∠A与∠B,∠C的度数即可得出答案.
解:设∠A、∠B、∠C分别为2x、3x、7x,
根据圆内接四边形对角互补有2x+7x=180°,
解得,x=20°,
∴∠B=3x=60°,
∴∠D=180°﹣∠B=120°,
故答案为:120.
-
科目: 来源: 题型:
查看答案和解析>>【题目】整式的加减运算:
(1)化简:-(x2+y2)+[-3xy-(x2-y2)];
(2)先化简,再求值:2(x2y+xy)-
 (x2y-
(x2y- xy)-4xy-x2y)其中x=1,y=-2
xy)-4xy-x2y)其中x=1,y=-2 -
科目: 来源: 题型:
查看答案和解析>>【题目】在建立平面直角坐标系的方格纸中,每个小方格都是边长为1的小正方形,△ABC的顶点均在格点上,点P的坐标为(﹣1,0),请按要求画图与作答.

(1)把△ABC绕点P旋转180°得△A′B′C′.
(2)把△ABC向右平移7个单位得△A″B″C″.
(3)△A′B′C′与△A″B″C″是否成中心对称,若是,找出对称中心P′,并写出其坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读材料:已知,如图(1),在面积为S的△ABC中, BC=a,AC=b, AB=c,内切圆O的半径为r连接OA、OB、OC,△ABC被划分为三个小三角形.
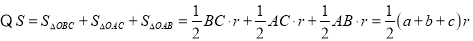
∴
 .
.
(1)类比推理:若面积为S的四边形ABCD存在内切圆(与各边都相切的圆),如图(2),各边长分别为AB=a,BC=b,CD=c,AD=d,求四边形的内切圆半径r;
(2)理解应用:如图(3),在等腰梯形ABCD中,AB∥DC,AB=21,CD=11,AD=13,⊙O1与⊙O2分别为△ABD与△BCD的内切圆,设它们的半径分别为r1和r2,求
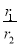 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】某国际化学校实行小班制教学,七年级四个班共有学生(6m-3n)人,一班有学生m人,二班人数比一班人数的两倍少n人,三班人数比二班人数的一半多12人.
(1)求三班的学生人数(用含m.n的式子表示);
(2)求四班的学生人数;(用含m.n的式子表示);
(3)若四个班共有学生120人,求二班比三班多的学生人数?
-
科目: 来源: 题型:
查看答案和解析>>【题目】⊙O的半径为6cm,点A到圆心O的距离为5cm,那么点A与⊙O的位置关系是( )
A.点A在圆内
B.点A在圆上
C.点A在圆外
D.不能确定 -
科目: 来源: 题型:
查看答案和解析>>【题目】国家规定“中小学生每天在校体育活动时间不低于1小时”,为了解学生参加体育活动的情况。调查了某校八年级甲、乙两班学生每天参加体育锻炼的时间,并将调查结果制成如下的频数分布表和频数分布直方图(数据包括左端点不包括右端点)。
甲班学生每天参加体育活动时间频数分布表分组(单位:h)
频数
0≤t<0.5
2
0.5≤t<1
10
1≤t<1.5
14
1.5≤t<2
12
2≤t<2.5
2

请你根据图表所提供的信息解答下列问题:
(1)如果每天在校体育活动时间不低于1小时为“达标”,求甲班学生每天在校体育活动时间的达标率。
(2)乙班学生每天参加体育活动时间的中位数落在在哪一组?
(3)请选择一个适当的统计量,对甲、乙两班学生每天参加体育活动的时间进行评价。
相关试题

