【题目】旋转变换在平面几何中有着广泛的应用.特别是在解(证)有关等腰三角形、正三角形、正方形等问题时,更是经常用到的思维方法,请你用旋转交换等知识,解决下面的问题.
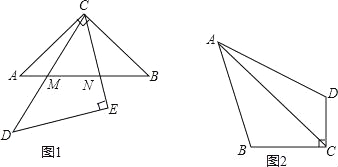
如图1,△ABC与△DCE均为等腰直角三角形,DC与AB交于点M,CE与AB交于点N.
(1)以点C为中心,将△ACM逆时针旋转90°,画出旋转后的△A′CM′
(2)在(1)的基础上,证明AM2+BN2=MN2.
(3)如图2,在四边形ABCD中,∠BAD=45°,∠BCD=90°,AC平分∠BCD,若BC=4,CD=3,则对角线AC的长度为多少?(直接写出结果即可,但在图中保留解决问题的过程中所作辅助线、标记的有关计算数据等)
参考答案:
【答案】(1)画图见解析;(2)证明见解析;(3) 6![]()
【解析】试题分析:(1)根据旋转的性质画出图形即可;(2)连接M'N,利用旋转的性质可得∠BCM'=∠ACM,CM=CM',AM=BM',∠CBM'=∠A=45°,和全等三角形的判再利用SAS证明△MCN≌△M'CN,根据全等三角形的性质可得MN=M'N,在RT△BM'N中,根据勾股定理得M'N2=BN2+BM'2,即可得MN2=AM2+BN2;
(3)将△ADC顺时针旋转90°到△AC'D',连接C'C,类比(2)的方法得到DB=D'B,在RT△BCD'中,由勾股定理求得AC的 长即可.
试题解析:
解:(1)旋转后的△A'CM'如图1所示:
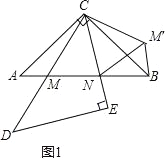
(2)连接M'N,
∵△ABC与△DCE为等腰直角三角形,∠ACB=90°,∠DCE=45°,
∴∠A=∠CBA=45°,∠ACM+∠BCN=45°,
∵△BCM'是由△ACM旋转得到的,
∴∠BCM'=∠ACM,CM=CM',AM=BM',∠CBM'=∠A=45°,
∴∠M'CN=∠MCN=45°,∠NBM'=90°,
∵CN=CN,
在△MCN与△M'CN中,
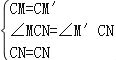 ,
,
∴△MCN≌△M'CN(SAS),
∴MN=M'N,
在RT△BM'N中,根据勾股定理得:M'N2=BN2+BM'2,
∴MN2=AM2+BN2;
(3)如图2,将△ADC顺时针旋转90°到△AC'D',连接C'C,
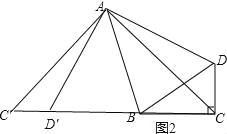
则△AC'C是等腰直角三角形,C'D=3,
∵∠C'=∠ACB=45°,
∴C',D',B,C均在同一直线上,
在△DAB与△D'AB中,
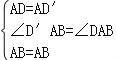 ,
,
∴△DAB≌△D'AB(SAS),
∴DB=D'B,
在RT△BCD'中,
∵BC=4,CD=3,
∴DB=5,
∴CC'=12,
∴AC=6![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】若关于x的一元二次方程为ax2+bx+6=0(a≠0)的解是x=1,则2016﹣a﹣b的值是( )
A.2020
B.2008
C.2014
D.2022 -
科目: 来源: 题型:
查看答案和解析>>【题目】下列关于x的方程中,一定是一元二次方程的为( )
A. ax2+bx+c=0B. x2 -2=(x+3)2C. x2 +3y 5=0D. x2-1=0
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图是用4个相同的小矩形与1个小正方形密铺而成的正方形图案,已知大正方形的面积为49,小正方形的面积为4,若用x,y(其中x>y)表示小矩形的长与宽,请观察图案,指出以下关系式中不正确的是( )
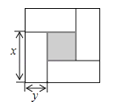
A.x+y=7
B.x﹣y=2
C.x2﹣y2=4
D.4xy+4=49 -
科目: 来源: 题型:
查看答案和解析>>【题目】一种零件的直径尺寸在图纸上是30±0.03(单位:mm),它表示这种零件的标准尺寸是30mm,加工要求尺寸最大不超过( )
A.0.03
B.0.02
C.30.03
D.29.98 -
科目: 来源: 题型:
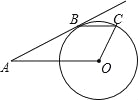
查看答案和解析>>【题目】如图,AB切⊙O于点B,OA=5
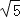 ,tanA=
,tanA=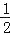 ,弦BC∥OA
,弦BC∥OA(1)求AB的长
(2)求四边形AOCB的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,二次函数y=﹣mx2+4m的顶点坐标为(0,2),矩形ABCD的顶点B.C在x轴上,A、D在抛物线上,矩形ABCD在抛物线与x轴所围成的图形内点A在点D的左侧.
(1)求二次函数的解析式;
(2)设点A的坐标为(x,y),试求矩形ABCD的周长P关于自变量x的函数解析式,并求出自变量x的取值范围;
(3)是否存在这样的矩形ABCD,使它的周长为9?试证明你的结论.

相关试题

