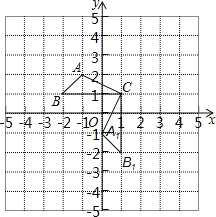
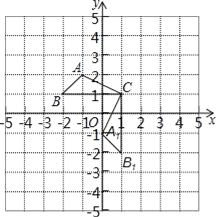
【题目】已知:△ABC在直角坐标平面内,三个顶点的坐标分别为A(﹣1,2)、B(﹣2,1)、C(1,1)(正方形网格中每个小正方形的边长是1个单位长度).
(1)△A1B1C1是△ABC绕点__逆时针旋转__度得到的,B1的坐标是__;
(2)求出线段AC旋转过程中所扫过的面积(结果保留π).
参考答案:
【答案】(1)C 90 (1,-2);(2)![]() .
.
【解析】(1)利用旋转的性质得出)△A1B1C1与△ABC的关系,进而得出答案;
(2)利用扇形面积求法得出答案.
解:(1)△A1B1C1是△ABC绕点C逆时针旋转90度得到的,
B1的坐标是:(1,﹣2),
故答案为:C,90,(1,﹣2);
(2)线段AC旋转过程中所扫过的面积为以点C为圆心,AC为半径的扇形的面积.
∵AC=![]() =
=![]() ,
,
∴面积为:![]() =
=![]() ,
,
即线段AC旋转过程中所扫过的面积为![]() .
.
“点睛”此题主要考查了扇形面积求法以及旋转变换,正确得出旋转角是解题关键.
-
科目: 来源: 题型:
查看答案和解析>>【题目】小红把1000元钱存入银行,整存整取3年,年利率是3.24%。到期时小红可得本金和利息一共________元.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知抛物线y=a(x﹣1)2﹣3(a≠0)的图象与y轴交于点A(0,﹣2),顶点为B.
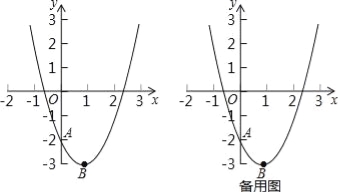
(1)试确定a的值,并写出B点的坐标;
(2)若一次函数的图象经过A、B两点,试写出一次函数的解析式;
(3)试在x轴上求一点P,使得△PAB的周长取最小值;
(4)若将抛物线平移m(m≠0)个单位,所得新抛物线的顶点记作C,与原抛物线的交点记作D,问:点O、C、D能否在同一条直线上?若能,请求出m的值;若不能,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】方程a2-16=0可化成两个一次方程是__________和___________;则x1=____,x2=____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB是⊙O的直径,C是⊙O上的一点,直线MN经过点C,过点A作直线MN的垂线,垂足为点D,且∠BAC=∠CAD.
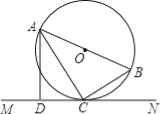
(1)求证:直线MN是⊙O的切线;
(2)若CD=3,∠CAD=30°,求⊙O的半径.
-
科目: 来源: 题型:
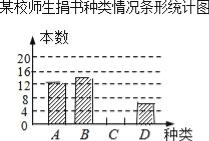
查看答案和解析>>【题目】在读书月活动中,某校号召全体师生积极捐书,为了解所捐书籍的种类,图书管理员对部分书籍进行了抽样调查,根据调查数据绘制了如下不完整的统计图表.请你根据统计图表所提供的信息回答下面问题:
某校师生捐书种类情况统计表
种类
频数
百分比
A.科普类
12
n
B.文学类
14
35%
C.艺术类
m
20%
D.其它类
6
15%
(1)统计表中的m= ,n= ;
(2)补全条形统计图;
(3)本次活动师生共捐书2000本,请估计有多少本科普类图书?
-
科目: 来源: 题型:
查看答案和解析>>【题目】“三次投掷一枚硬币,三次正面朝上”这一事件是( )
A.必然事件
B.随机事件
C.不可能事件
D.确定事件
相关试题

