【题目】在平面直角坐标系中,抛物线y=ax2+bx+3经过点A(3,0)和点B(4,3).
(1)求这条抛物线所对应的二次函数的表达式.
(2)直接写出该抛物线开口方向和顶点坐标.
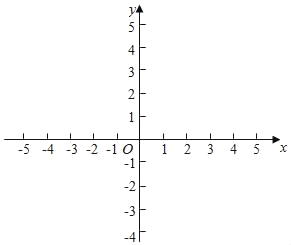
(3)直接在所给坐标平面内画出这条抛物线.
参考答案:
【答案】(1)y=x2﹣4x+3(2)(2,﹣1)(3)见解析
【解析】
(1)把A点和B点坐标代入y=ax2+bx+3得关于a、b的方程组,然后解方程组即可;
(2)先把一般式配成顶点式,然后根据二次函数的性质解决问题;
(3)利用描点法画函数图象.
(1)∵抛物线y=ax2+bx+3经过点A(3,0)和点B(4,3).
∴![]() ,解得
,解得![]() ,
,
∴这条抛物线所对应的二次函数的表达式为y=x2﹣4x+3;
(2)a=1>0,抛物线开口向上,
∵y=(x﹣2)2﹣1,
∴抛物线顶点坐标为(2,﹣1);
(3)如图,
-
科目: 来源: 题型:
查看答案和解析>>【题目】某校九年级举行毕业典礼,需要从九年(1)班的2名男生1名女生(男生用A1表示,女生用B1表示)和九年(2)班的1名男生1名女生(男生用A2表示,女生用B2表示)共5人中随机选出2名主持人.
(1)用树状图或列表法列出所有可能情形;
(2)求2名主持人来自不同班级的概率;
(3)求2名主持人恰好1男1女的概率.
-
科目: 来源: 题型:
查看答案和解析>>【题目】小明为了检验两枚六个面分别刻有点数1、 2、3、4、5、6的正六面体骰子的质量是否都合格,在相同的条件下,同时抛两枚骰子20 00 0次,结果发现两个朝上面的点数和是7的次数为20次.你认为这两枚骰子质量是否都合格(合格标准为:在相同条件下抛骰子时,骰子各个面朝上的机会相等)?并说明理由.
-
科目: 来源: 题型:
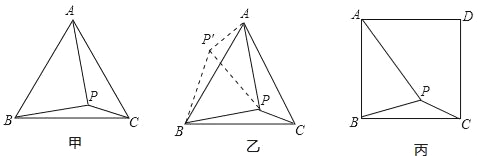
查看答案和解析>>【题目】如图甲,在等边三角形ABC内有一点P,且PA=2,PB=
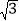 ,PC=1,求∠BPC度数的大小和等边三角形ABC的边长.
,PC=1,求∠BPC度数的大小和等边三角形ABC的边长.解题思路是:将△BPC绕点B逆时针旋转60°,如图乙所示,连接PP′.
(1)△P′PB是 三角形,△PP′A是 三角形,∠BPC= °;
(2)利用△BPC可以求出△ABC的边长为 .
如图丙,在正方形ABCD内有一点P,且PA=
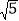 ,BP=
,BP= ,PC=1;
,PC=1;(3)求∠BPC度数的大小;
(4)求正方形ABCD的边长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,线段AB经过圆心O,交⊙O于点A、C,点D为⊙O上一点,连结AD、OD、BD,∠BAD=∠B=30°.
(1)求证:BD是⊙O的切线.
(2)若OA=8,求OA、OD与
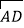 围成的扇形的面积.
围成的扇形的面积.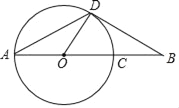
-
科目: 来源: 题型:
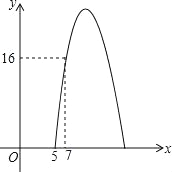
查看答案和解析>>【题目】某种商品每天的销售利润y(元)与销售单价x(元)之间满足关系y=mx2+20x+n,其图象如图所示.
(1)m=_____,n=_____.
(2)销售单价为多少元时,该种商品每天的销售利润最大?最大利润为多少元?
(3)该种商品每天的销售利润不低于16元时,直接写出x的取值范围.
-
科目: 来源: 题型:
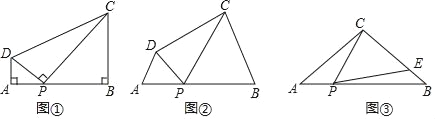
查看答案和解析>>【题目】(感知)如图①,在四边形ABCD中,点P在边AB上(点P不与点A、B重合),∠A=∠B=∠DPC=90°.易证:△DAP∽△PBC(不要求证明).
(探究)如图②,在四边形ABCD中,点P在边AB上(点P不与点A、B重合),∠A=∠B=∠DPC.
(1)求证:△DAP~△PBC.
(2)若PD=5,PC=10,BC=9,求AP的长.
(应用)如图③,在△ABC中,AC=BC=4,AB=6,点P在边AB上(点P不与点A、B重合),连结CP,作∠CPE=∠A,PE与边BC交于点E.当CE=3EB时,求AP的长.
相关试题

