【题目】(本小题满分14分)
如图,直线y=kx+b(k、b为常数)分别与x轴、y轴交于点A(-4,0)、B(0,3),抛物线y=-x2+2x+1与y轴交于点C.
(1)求直线y=kx+b的解析式;
(2)若点P(x,y)是抛物线y=-x2+2x+1上的任意一点,设点P到直线AB的距离为d,求d关于x的函数解析式,并求d取最小值时点P的坐标;
(3)若点E在抛物线y=-x2+2x+1的对称轴上移动,点F在直线AB上移动,求CE+EF的最小值. 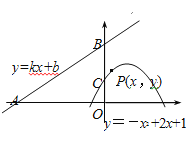
参考答案:
【答案】(1) y=![]() x+3;(2)P(
x+3;(2)P(![]() ,
,![]() );(3)
);(3)![]() .
.
【解析】
试题分析:(1)将A、B两点坐标代入y=kx+b中,求出k、b的值;(2)作出点P到直线AB的距离后,由于∠AHC=90°,考虑构造“K形”相似,得到△MAH、△OBA、△NHP三个三角形两两相似,三边之比都是3∶4∶5.由“![]() ”可得
”可得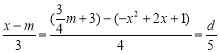 ,整理可得d关于x的二次函数,配方可求出d的最小值;(3)如果点C关于直线x=1的对称点C′,根据对称性可知,CE=C′E.当C′F⊥AB时,CE+EF最小.
,整理可得d关于x的二次函数,配方可求出d的最小值;(3)如果点C关于直线x=1的对称点C′,根据对称性可知,CE=C′E.当C′F⊥AB时,CE+EF最小.
试题解析:
解:(1)∵y=kx+b经过A(-4,0)、B(0,3),
∴![]() ,解得k=
,解得k=![]() ,b=3.
,b=3.
∴y=![]() x+3.
x+3.
(2)过点P作PH⊥AB于点H,过点H作x轴的平行线MN,分别过点A、P作MN的垂线段,垂足分别为M、N.
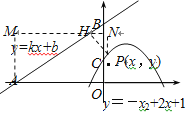
设H(m,![]() m+3),则M(-4,
m+3),则M(-4,![]() m+3),N(x,
m+3),N(x,![]() m+3),P(x,-x2+2x+1).
m+3),P(x,-x2+2x+1).
∵PH⊥AB,∴∠CHN+∠AHM=90°,∵AM⊥MN,∴∠MAH+∠AHM=90°.
∴∠MAH=∠CHN,∵∠AMH=∠CNH=90°,∴△AMH∽△HNP.
∵MA∥y轴,∴△MAH∽△OBA.∴△OBA∽△NHP.
∴![]() .
.
∴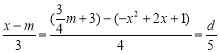 .
.
整理得:![]() ,所以当x=
,所以当x=![]() ,即P(
,即P(![]() ,
,![]() ).
).
(3)作点C关于直线x=1的对称点C′,过点C′作C′F⊥AB于F.过点F作JK∥x轴,,分别过点A、C′作J⊥JK于点J,C′K⊥JK于点K.则C′(2,1)
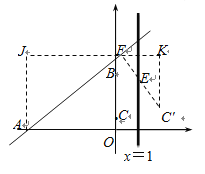
设F(m,![]() m+3)
m+3)
∵C′F⊥AB,∠AFJ+∠C′FK=90°,∵CK⊥JK,∴∠C′+∠C′FK=90°.
∴∠C′=∠AFJ,∵∠J=∠K=90°,∴△AFJ∽△FC′K.
∴![]() ,∴
,∴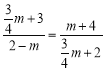 ,解得m=
,解得m=![]() 或-4(不符合题意).
或-4(不符合题意).
∴F(![]() ,
,![]() ),∵C′(2,1),∴FC′=
),∵C′(2,1),∴FC′=![]() .
.
∴CE+EF的最小值=C′E=![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】公路上一辆汽车以50km/h的速度匀速行驶,它行驶的时间与路程这两个量中,__是自变量,__是因变量.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(本小题满分10分)
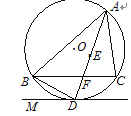
如图,点E是△ABC的内心,AE的延长线交BC于点F,交△ABC的外接圆⊙O于点D;连接BD,过点D作直线DM,使∠BDM=∠DAC.
(1)求证:直线DM是⊙O的切线;
(2)求证:DE2=DF·DA.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,边长为2的正方形ABCD在第一象限内,AB∥x轴,点A的坐标为(5,3),己知直线l:y=
 x﹣2
x﹣2 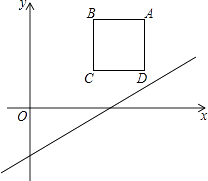
(1)将直线l向上平移m个单位,使平移后的直线恰好经过点A,求m的值
(2)在(1)的条件下,平移后的直线与正方形的边长BC交于点E,求△ABE的面积. -
科目: 来源: 题型:
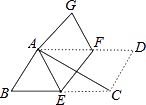
查看答案和解析>>【题目】在ABCD中,∠ACB=25°,现将ABCD沿EF折叠,使点C与点A重合,点D落在G处,则∠GFE的度数( )
A.135°
B.120°
C.115°
D.100° -
科目: 来源: 题型:
查看答案和解析>>【题目】某市的出租车收费按里程计算,3km内(含3km)收费5元,超过3km,每增加1km加收1元,则路程x≥3时,车费y(元)与x(km)之间的关系式是_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】9x2﹣mxy+16y2是一个完全平方式,则m的值为 .
相关试题

