【题目】已知![]() 、
、![]() 两地之间有一条270千米的公路,甲、乙两车同时出发,甲车以每小时60千米/时的速度沿此公路从
两地之间有一条270千米的公路,甲、乙两车同时出发,甲车以每小时60千米/时的速度沿此公路从![]() 地匀速开往
地匀速开往![]() 地,乙车从
地,乙车从![]() 地沿此公路匀速开往
地沿此公路匀速开往![]() 地,两车分别到达目的地后停止甲、乙两车相距的路程
地,两车分别到达目的地后停止甲、乙两车相距的路程![]() (千米)与甲车的行驶时间
(千米)与甲车的行驶时间![]() (时)之间的函数关系如图所示:
(时)之间的函数关系如图所示:
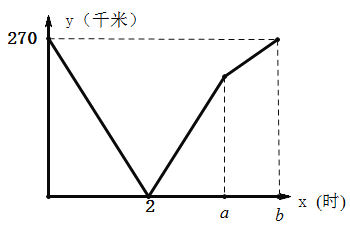
(1)乙年的速度为______千米/时,![]() _____,
_____,![]() ______.
______.
(2)求甲、乙两车相遇后![]() 与
与![]() 之间的函数关系式,并写出相应的自变量
之间的函数关系式,并写出相应的自变量![]() 的取值范围.
的取值范围.
【答案】(1)75;3.6;4.5;(2) 当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]() .
.
【解析】
(1)根据图像可知两车2小时候相遇,根据路程和为270千米即可求出乙车的速度,然后根据“路程、速度、时间”的关系确定![]() 、b的值;
、b的值;
(2)根据图像可知相遇后图像分为两段,将相遇后点的坐标和分段处以及到达B地后的坐标分别表示出来,然后运用待定系数法解决即可;
解:(1)乙车的速度为:(270-60×2)÷2=75(千米/时);
![]() =270÷75=3.6,b=270÷60=4.5
=270÷75=3.6,b=270÷60=4.5
故答案为:75;3.6;4.5;
(2)60×3.6=216(千米),如图,可得![]() ,
,![]() ,
,![]() .
.
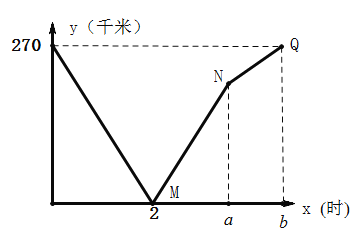
设当![]() 时的解析式为
时的解析式为![]() ,
,
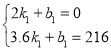 ,
,
解得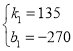
![]() 当
当![]() 时,
时,![]() ,
,
设当![]() 时的解析式为
时的解析式为![]() ,则
,则
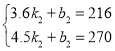 ,
,
解得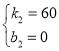 ,
,
当![]() 时,
时,![]() .
.

